报告题目: Gaussian Random Fields and Random Fractals
报 告人: 肖益民教授(美国密西根州立大学)
报告时间: 2023年1月 9、10、11 日(星期一、二、三)上午 09:00-12:00
报告地点:腾讯会议:997-8632-4384
邀 请人: 匡锐副教授
欢迎广大师生前往!
数学学院
2023年1月4日
报告摘要: Multivariate random fields have recently been the focus of much attention in probability and statistics, due to their extensive applications as spatial or spatio-temporal models in scientific areas where many problems involve data sets with multivariate measurements obtained at spatial locations. Several classes of multivariate Gaussian random fields have been introduced and studied in the literature. Many of these random fields have interesting statistical self-similarity or other scaling properties which make tools from fractal geometry useful for characterizing their sample path properties. See. for example,
In our lectures, we plan to cover the following topics:
(i) Multivariate random fields, self-similarity, operator-scaling properties
The mathematical theory of random fields developed by Itô (1954), Yaglom (1957, 1987), Gihman and Skorohod (1974) provides an excellent framework for constructing and studying multivariate random fields. This lecture will introduce systematic methods for constructing univariate and multivariate Gaussian random fields, including characterization of cross-covariance matrices and the spectral method. Interesting examples of multivariate Gaussian random fields that can be constructed by using these methods include multivariate stationary Gaussian random fields with Matérn cross-covariance matrix and operator fractional Brownian motion.
We will characterize their important statistical properties such as self-similarity and operator-scaling properties.
(ii) Computation of Hausdorff, packing, and intermediate dimensions
We compute Hausdorff, packing, and intermediate dimensions of random fractals generated by Gaussian random fields including the range, graph, level sets, and set of multiple points.
(iii) Hitting probabilities of Gaussian random fields [2]
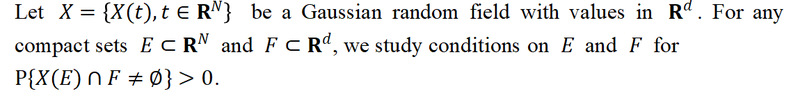
Only in a few special cases, this hitting probability problem has been solved. We will present the necessary and sufficient conditions due to Khoshnevisan and Shi (1999), Khoshnevisan and Xiao (2007, 2015), Biermé, Lacaux and Xiao (2009), Dalang, Mueller, and Xiao (2017), Lee, Song, Xiao and Yuan (2022).
(iv) Regularity of Gaussian random fields and exact uniform and local moduli of continuity
Regularity properties such as continuity and differentiability of the sample functions of Gaussian processes are important topics in probability theory and essential for statistical applications.
Necessary and sufficient conditions for sample path continuity based on the metric entropy or majorizing measure were established by Dudley (1967), Fernique (1975), and Talagrand (1987).
The purpose of this module is to present methods for establishing exact uniform and local modulus of continuity results for Gaussian random fields. The main technical tool is the property of strong local nondeterminism. These results are from Wang, Su and Xiao (2020), Lee and Xiao (2022).
References
[1] Biermé, H., Lacaux, C. and Xiao, Y., Hitting probabilities and the Hausdorff dimension of the inverse images of anisotropic Gaussian random fields. Bull. London Math. Soc. 41 (2009), 253-273.
[2] Dalang, R. C., Mueller, C. and Xiao, Y., Polarity of points for Gaussian random fields. Ann. Probab. 45(2017), 4700-4751.
[3] Dudley, R. M., Sample function of the Gaussian process. Ann. Probab. 1 (1973), 66-103.
[4] Gihman, I. I. and Skorohod, A. V., The Theory of Stochastic Processes, vol. 1. Springer-Verlag, Berlin, 1974.
[5] Itô, K., Stationary random distributions. Mem. Coll. Sci., Univ. Kyoto, Ser. 1: Math 28 (1954), 291-326.
[6] Khoshnevisan, D. and Shi, Z., Brownian sheet and capacity. Ann. Probab. 27 (1999), 1135-1159.
[7] Khoshnevisan, D.,Wu, D. and Xiao, Y., Sectorial local non-determinism and the geometry of the Brownian sheet. Electronic J. Probab. 11 (2006), 817-843.
[8] Khoshnevisan, D. and Xiao, Y., Images of the Brownian sheet. Trans. Amer. Math. Soc. 359 (2007), 3125-3151.
[9] Khoshnevisan, D. and Xiao, Y., Brownian motion and thermal capacity. Ann. Probab. 43 (2015), 405-434.
[10] Lee, C-Y., Song, J., Xiao, Y. and Yuan, W. Hitting probability of Gaussian random fields with application to collision of eigenvalues of random matrices. Submitted, 2022.
[11] Lee, C-Y. and Xiao, Y. Chung-type law of the iterated logarithm and exact moduli of continuity for a class of anisotropic Gaussian random fields. Bernoulli, to appear.
[12] Talagrand, M., Regularity of Gaussian processes. Acta Math. 159 (1987),
99-149.
[13] Wang, W., Su, Z. and Xiao, Y. The moduli of non-differentiability and local times of Gaussian random fields with stationary increments. Bernoulli 26 (2020), 1410-1430.
[14] Yaglom, A. M., Some classes of random fields in n-dimensional space, related to stationary random processes. Th. Probab. Appl. 2 (1957), 273-320.
[15] Yaglom, A. M., Correlation Theory of Stationary and Related Random Functions, Vol. 1. Springer-Verlag, New York, 1987.
报告人简介:肖益民教授主要从事随机过程,随机场(特别是Levy过程,高斯场)及随机偏微分方程解的几何性质和位势理论等方面的研究。在下列几方面取得了一系列具有国际先进水平的研究成果:
(1)运用分形几何的工具,对高斯随机场及一般具有无穷可分分布的随机场的样本轨道性质进行刻画。特别是运用“强局部不确定性”对高斯场的局部时理论,精确连续模及分形测度函数等方面进行研究,其方法已被用于研究随机偏微分方程解的性质。
(2)在随机场的位势理论方面,与Utah大学的Davar Khoshnevisan教授合作,发展了可加Levy过程和Brown单的位势理论,建立了各种“击中”概率与“解析容度”之间的对应关系。该理论不仅是随机场理论中重要的组成部分,而且为研究通常马氏过程,特别是为Levy过程样本轨道性质的研究提供了有力的工具。
(3)在Levy过程的样本轨道研究方面,与Davar Khoshnevisan教授合作,运用可加随机场的位势理论,解决了一系列关于Levy过程自1969年以来遗留下来的、由著名概率论学家W.E.Pruitt(1969)、J.-P. Kahane(1983)和Jean Bertoin(1999)等人提出的公开问题,其中包括一般Levy过程的象集的Hausdorff维数的计算公式,Levy过程在一般紧集上相交性的判别法及再生集合相交性的判别法。
由于在随机场理论方面做出的学术贡献,肖益民教授于2011年当选为Fellow of the Institute of Mathematical Statistics。肖益民教授是密西根州立大学统计学院首席教授,同时担任《Statistics and Probability Letters》、《Illinois Journal of Mathematics》、《Science in China, Mathematics》等期刊的主编或编委。持续在Annals of Probability,Probability Theory and Related Fields,Comm. Math. Physics等国际一流期刊发表论文。
