学术报告报告题目: DC ALGORITHMS FOR A CLASS OF SPARSE GROUP
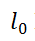
REGULARIZED OPTIMIZATION PROBLEMS
报 告人: 边伟 教授
报告时间: 2022年3月28日（星期一下午）15:00-16:00
报告地点： 腾讯会议号：137-248-694 会议密码：220328
https: //meeting.tencent.com/dm/WiARYmFzaj3o
邀 请人: 潘少华教授
欢迎广大师生前往！
数学学院
2022年3月24日
报告摘要：In this talk, we consider a class of sparse group
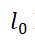regularized optimization problems. Firstly, we give a continuous relaxation model of the considered problem and establish the equivalence of these two problems in the sense of global minimizers. Then, we define a class of stationary points of the relaxation problem, and prove that any defined stationary point is a local minimizer of the considered sparse group
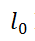regularized problem and satisfies a desirable property of its global minimizers. Further, based on the difference-of-convex (DC) structure of the relaxation problem, we design two DC algorithms to solve the relaxation problem. We prove that any accumulation point of the iterates generated by them is a stationary point of the relaxation problem. In particular, all accumulation points have a common support set and a unified lower bound for the nonzero entries, and their zero entries can be attained within finite iterations. Moreover, we prove the convergence of the entire iterates generated by the proposed algorithms. Finally, we give some numerical experiments to show the efficiency of the proposed algorithms.
报告人简介：边伟，哈尔滨工业大学数学学院，教授、博士生导师。主要从事的研究领域为：最优化理论与算法、神经网络。先后在 MP, SIOPT, SIIMS, SINUA，SISC, MOR和三个IEEE系列汇刊发表多篇学术论文。先后获得2018年度 “龙江青年学者”和2019年度教育部青年学者称号。主持国家自然科学基金面上项目2项和青年基金项目1项。获得黑龙江省自然科学二等奖（排第二）一项。任中国运筹学会理事，中国运筹学会数学规划分会理事，黑龙江数学会常务理事，任SCI期刊JOTA编委。