报告题目:The universality of the semi-classical sine-Gordon equation at the gradient catastrophe
报 告人:Bingling-Lu (University of Bremen)
报告时间:2021年 9月 18日(星期 六)下午 3:00-4:00
报告地点:腾讯会议,会议号:188 881 201
邀 请人:凌黎明教授
欢迎广大师生前往!
数学学院
2021年 9 月 13 日
报告摘要:We study the semi-classical sine-Gordon equation with pure impulse initial data below the threshold of rotation:
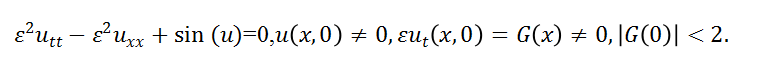
A dispersively-regularized shock forms in finite time. Using Riemann–Hilbert analysis, we rigorously studied the asymptotics near a certain gradient catastrophe. In accordance with a conjecture made by Dubrovin et. al., the asymptotics in the this region is universally (insensitive to initial condition) described by the tritronquee solution to the Painleve-I equation. Furthermore, we are able to universally characterize the shapes of the spike-like local structures (rogue wave on periodic background) on top of the poles of the tritronqu\’ee solution.
报告人简介:Bingling Lu, 本科毕业于上海交通大学,博士毕业于University of Michigan, 博士毕业之后在台湾大学中央研究院从事博士后研究,现任职于University of Bremen. Bingling-Lu长期从事于Riemann-Hilbert渐近性的研究,尤其是半经典极限的分析。 在数学权威期刊“Communications on Pure and Applied Mathematics”发表文章。
