原文标题：Learning-Based Temporal Sequence of Constrained Handling Selection for Constrained Multi-objective Evolutionary Optimization

原文作者：Chaoda Peng, Siyuan Yan, Cankun Zhong, Qiong Huang, Chunguo Wu, Han Huang*

原文期刊：IEEE Transactions on Evolutionary Computation

原文链接：https://ieeexplore.ieee.org/abstract/document/11058982

原文发表时间：2025年6月

摘要

约束处理技术（CHTs）和遗传算子是约束多目标进化算法（CMOEAs）中的两个核心组成部分。当前CMOEAs研究主要专注于这些组件的自适应设计，以应对不同的约束多目标优化问题（CMOPs）。然而，求解CMOP的进化过程涉及多种特征，例如连续性、离散性、退化性等，这就需要在不同的进化代次中有针对性地选择合适的CHTs和遗传算子。本研究将这种选择过程概念化为约束处理选择的时间序列，其中时间维度对应于种群的进化代数。我们认为，通过分析不同选择策略的历史应用数据来挖掘该序列中的系统性规律，能够显著提升CMOEAs发现帕累托最优解的性能。基于这一理念，我们提出了一种融合深度强化学习模型的CMOEA来求解CMOPs。具体来说，该深度强化学习模型能够从以往选择策略的性能表现中学习经验，动态优化后续代次中CHTs和遗传算子的选择，进而提高选择策略的预测精度。在37个基准测试问题和一个无人机路径规划实际应用问题上的实验结果表明，所提出的CMOEA-TS算法相比九种现有的CMOEAs表现出显著的性能优势。实验结果验证了挖掘时间序列中系统性模式对于CMOEAs在目标优化和约束满足两个方面求解CMOPs的积极促进作用。

• 研究背景

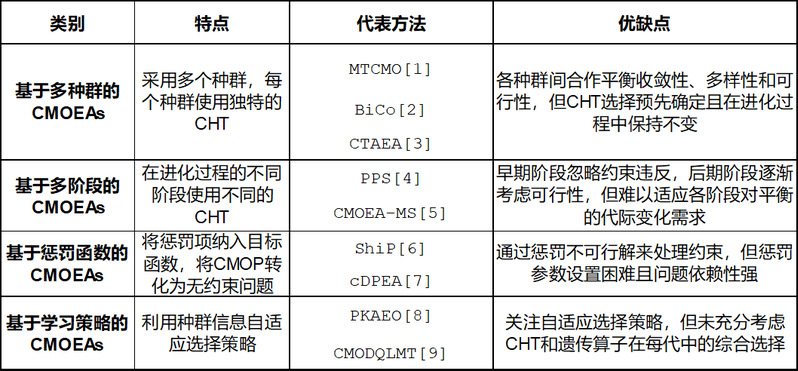
约束多目标优化问题（CMOPs）广泛存在于现实世界的各种应用场景中，如物联网应用、自主车辆路径规划、模拟电路设计和短期原油调度等。近期CMOEAs研究可分为四个类别，具体如下表所示：

现有四类CMOEAs均存在一个共同局限：缺乏对CHT和遗传算子在每一代中动态选择的系统性考虑。本研究提出将整个进化过程中的选择策略建模为约束处理选择的时间序列，其中时间维度对应进化代数。值得注意的是，从本质上讲，现有的自适应CMOEAs可以被视为该时间序列框架下的一个特殊实例。

二. 基于约束处理选择时间序列的CMOEA-TS算法

A. 约束处理选择时间序列的基础定义

基于定义1，现有的设计自适应CHT和算子的CMOEAs可以被视为约束处理选择时间序列模型中的特殊实例。例如，基于多阶段的CMOEAs在进化过程的不同阶段采用多个CHT，这些CHT在整个进化过程中的采用形成了约束处理选择时间序列，其中每个阶段对应于我们模型中时间序列的特定片段。

B. 基于深度强化学习的约束处理选择时间序列

考虑到CHT和遗传算子在每代中从A中选择，可能选择路径的总数随着代数呈指数级增长。因此，识别序列中的系统模式是一项计算密集的任务。在这种情况下，强化学习在缓解这一计算挑战方面发挥着关键作用，它使智能体能够基于进化过程的反馈动态调整其策略。

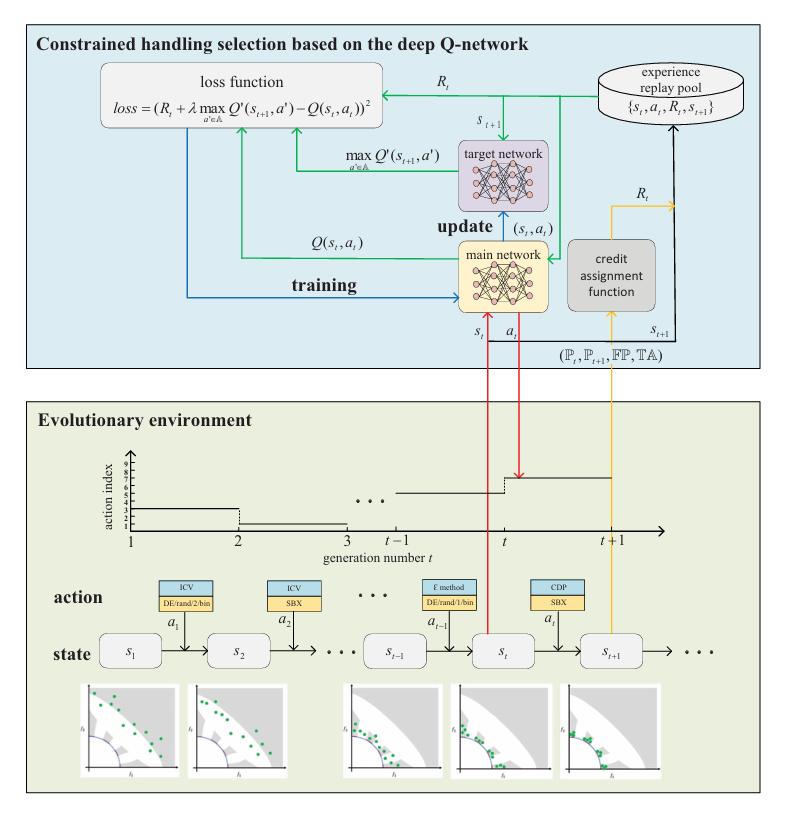
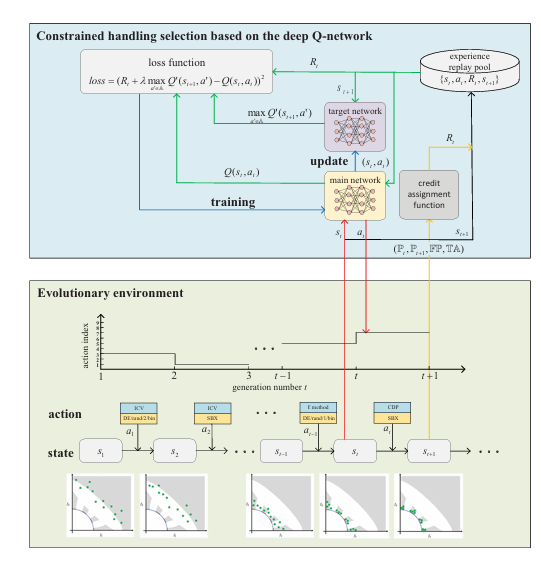
如图1所示，本文利用深度Q网络来寻求约束处理选择时间序列中的结构化模式。深度Q网络将CHT和遗传算子的选择特征化为动作，以特定的种群信息作为状态。此外，它通过测量两个连续种群之间目标优化和约束满足的改进来确定奖励。

整体框架由四个关键组件构成：

这种设计使得算法能够在线学习最优的约束处理策略组合，相比现有方法实现了CHT和遗传算子的综合自适应选择。

C. CMOEA-TS进化算法框架

基于上述深度强化学习模型，CMOEA-TS采用增强的代际进化框架，具体流程如下：

初始化阶段：

随机生成初始种群P₁，初始化主网络Q和目标网络Q'

建立临时档案TA和输出档案FP，创建空的经验回放池E

迭代进化过程（每代t执行）：

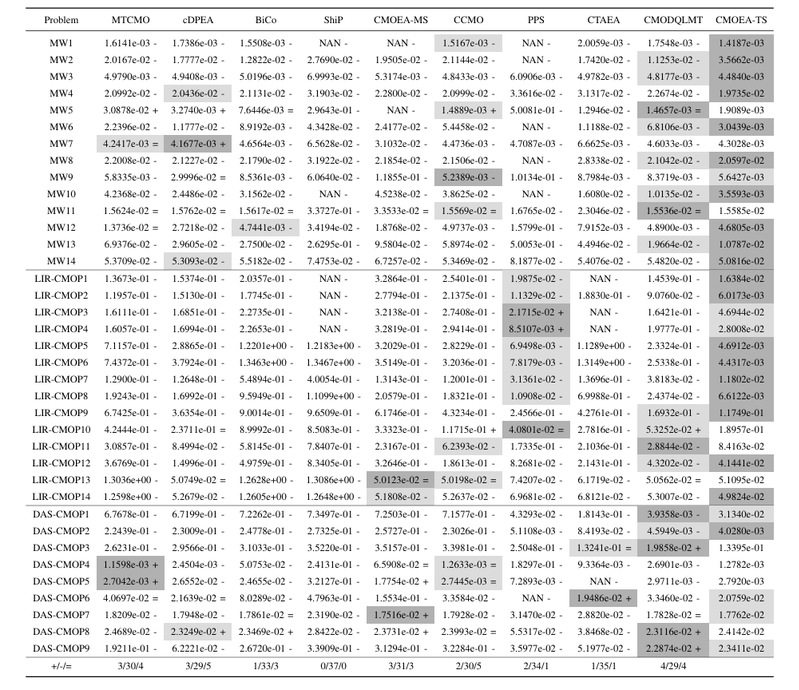
三. 实验结果

本文在三个广泛使用的基准测试集上验证CMOEA-TS的性能，即MW、LIR-CMOP和DAS-CMOP，并与九种先进的CMOEAs进行对比，包括MTCMO、cDPEA、BiCo、ShiP、CMOEA-MS、CCMO、PPS、CTAEA和CMODQLMT。

实验设置

• 种群规模：二目标问题设为100，三目标问题设为300

• 终止条件：MW问题最大代数1000，LIR-CMOP和DAS-CMOP问题最大代数1500

• 独立运行次数：每个算法在每个测试问题上独立运行30次

• 性能指标：采用IGD和HV两个指标评估算法性能

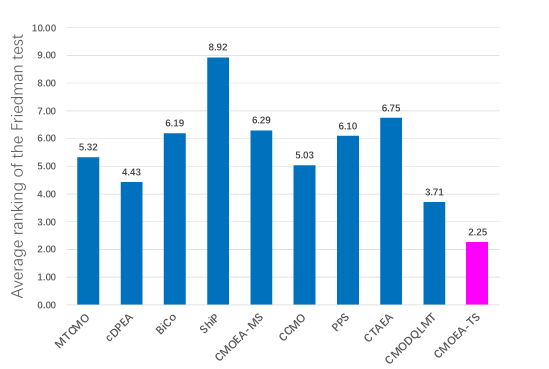
（1）总体性能实验结果如下所示：

下图展示的Friedman统计检验平均排名结果表明，CMOEA-TS以2.25的最低排名位列第一，显著优于其他九种对比算法。

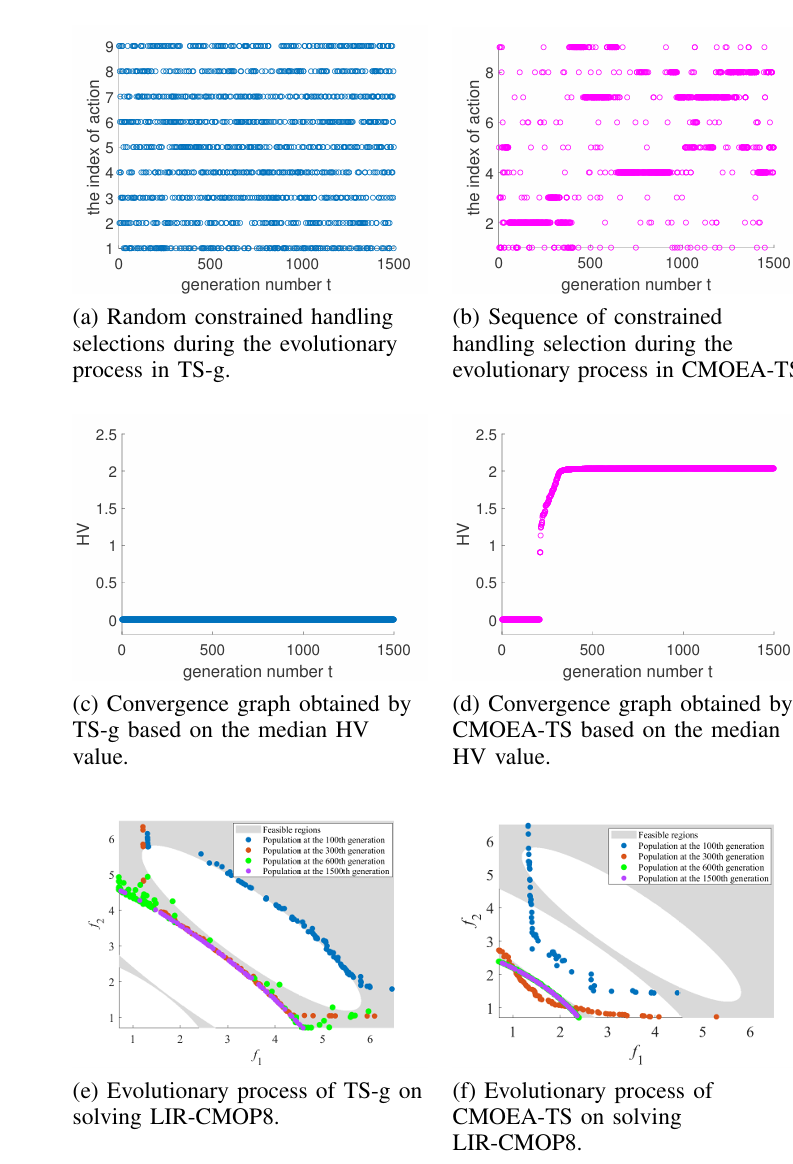
（2）模式发现验证

下图展示了CMOEA-TS在LIR-CMOP8上的约束处理选择序列演化过程。结果表明，算法能够从早期的随机探索逐渐收敛到有效的选择模式，验证了时间序列模式发现的有效性。

实验结果充分证明了发现约束处理选择时间序列中系统性模式对于提升CMOEA性能的积极作用。

四.结论

本研究的主要创新点总结如下：

1）提出了约束处理选择时间序列的新概念：将CHT和遗传算子的选择过程建模为时间序列，为理解和改进现有CMOEAs提供了统一的理论框架，现有自适应方法可视为该框架下的特殊实例。

2）构建了动态策略组合选择机制：通过深度强化学习模型从历史选择数据中挖掘有效模式，实现CHT和遗传算子的在线自适应选择，改进了现有方法在策略选择上的不足。

参考文献：[1] K. Qiao, K. Yu, B. Qu, J. Liang, H. Song, C. Yue, H. Lin, and K. C. Tan, Dynamic auxiliary task-based evolutionary multitasking for constrained multi-objective optimization, IEEE Transactions on Evolutionary Computation, vol. 27, no. 3, pp. 642–656, 2023.

[2] Z.-Z. Liu, B.-C. Wang, and K. Tang, Handling constrained multiobjective optimization problems via bidirectional coevolution, IEEE Transactions on Cybernetics, vol. 52, no. 10, pp. 10 163–10 176, 2022.

[3] K. Li, R. Chen, G. Fu, and X. Yao, Two-archive evolutionary algorithm for constrained multiobjective optimization, IEEE Transactions on Evolutionary Computation, vol. 23, no. 2, pp. 303–315, 2019.

[4] Z. Fan, W. Li, X. Cai, H. Li, C. Wei, Q. Zhang, K. Deb, and E. Goodman, Push and pull search for solving constrained multi-objective optimization problems, Swarm and Evolutionary Computation, vol. 44, pp. 665–679, 2019.

[5] Y. Tian, Y. Zhang, Y. Su, X. Zhang, K. C. Tan, and Y. Jin, Balancing objective optimization and constraint satisfaction in constrained evolutionary multiobjective optimization, IEEE Transactions on Cybernetics, vol. 52, no. 9, pp. 9559–9572, 2022.

[6] Z. Ma and Y. Wang, Shift-based penalty for evolutionary constrained multiobjective optimization and its application, IEEE Transactions on Cybernetics, vol. 53, no. 1, pp. 18–30, 2023.

[7] C. Wang, Z. Wang, Y. Tian, X. Zhang, and J. Xiao, A dual-population based evolutionary algorithm for multi-objective location problem under uncertainty of facilities, IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 7, pp. 7692–7707, 2022.

[8] M. Zuo, D. Gong, Y. Wang, X. Ye, B. Zeng, and F. Meng, Process knowledge-guided autonomous evolutionary optimization for constrained multiobjective problems, IEEE Transactions on Evolutionary Computation, vol. 28, no. 1, pp. 193–207, 2024.

[9] F. Ming, W. Gong, and L. Gao, Adaptive auxiliary task selection for multitasking-assisted constrained multi-objective optimization, IEEE Computational Intelligence Magazine, vol. 18, no. 2, pp. 18–30, 2023.