| 微搜索使约束优化不再是难题 |
| 发布时间: 2024-12-27 浏览次数: 10 |
|
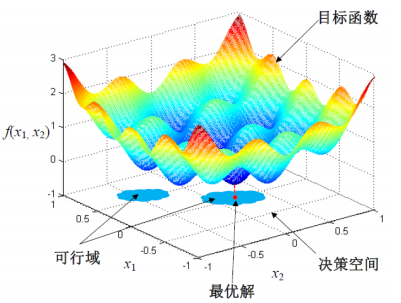
一、关于约束优化问题 约束优化问题(Constrained Optimization Problem, COP)是指在一组约束条件下,寻找一个或多个变量的值,使得某个目标函数达到最优值(最大值或最小值)的问题。约束优化问题在数学、工程、经济和管理等领域都有广泛的应用。比如说:如何以最省钱的方式尽快到达目的地,如何以最低的造价建造一栋高安全性的大厦。以最小化的优化目标为例,约束优化问题可以定义如下:
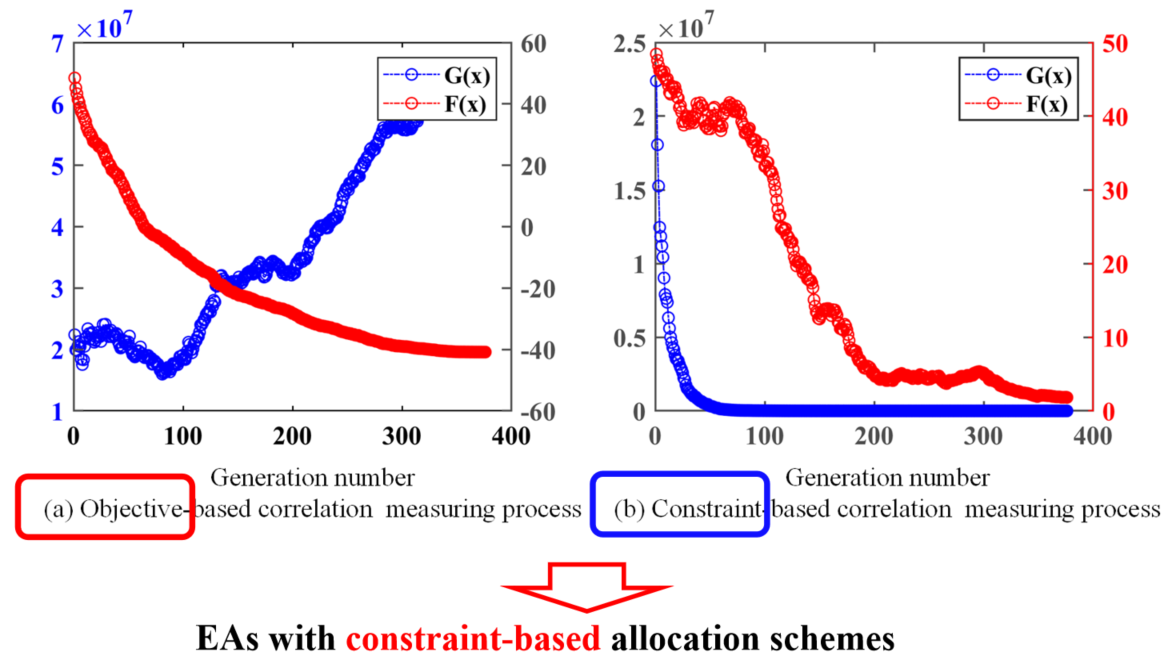
图1 约束优化问题三维图 在进化计算领域,约束优化问题一直是一个备受关注的研究热点。所谓约束优化,就是在优化目标函数的同时,还需要满足一定的约束条件。这使得问题的求解过程变得复杂。传统约束进化算法通常采用预先设定的无偏好、目标偏好、或约束偏好比较准则来实现在目标优化和约束处理上的算力(适应度评估次数)分配方案。基于约束偏好算力分配方案的算法主要专注搜索可行域。而基于目标偏好分配方案的算法则可以忽略对约束的处理,专注搜索无约束最优解所在位置,在面对复杂约束条件的问题且无约束最优解接近最优解的问题时,有利于帮助算法搜索最优解。然而,由于不同的 COP 最优解所在区域、无约束最优解所在区域和部分可行域的位置各不相同,基于预先设定偏好算力分配方案的算法容易造成算力浪费或难以搜索到最优解的问题。 考虑到不同算力分配方案的算法在潜在搜索范围上有差异,我们可以基于不同偏好的算力分配方案,将决策集划分为多个决策子集 (见定义1),并根据微搜索思想[1],预估出包含最优解且测度小于原始决策集规模的潜在决策子集 (有效决策子集,见定义2),在有效决策子集内进行搜索,避免算力浪费。这里的决策子集由算法在遵循不同偏好比较准则的搜索路径下所覆盖的解集构成。 定义1 (决策子集): 假设约束优化问题的决策集为 。如果 ,则称集合为该优化问题的决策子集。 定义2 (有效决策子集): 假设决策集为, 为 的决策子集。如果,且存在一个最优解 ,则称决策子集 为该优化问题的有效决策子集。 根据定义,当满足以下两个条件时决策子集为有效决策子集: (1) 决策子集的规模小于决策集; (2) 决策子集包含最优解。对于约束优化算法而言,在目标优化和约束处理的算力分配方案很大程度上决定了算法的搜索空间。如果最优解在无约束最优解所在区域,无约束最优解的小范围邻域则为有效决策子集,那么在有限的评估次数内,基于目标偏好比较准则的约束进化算法在性能上可以得到提升。本研究认为,基于目标偏好和基于约束偏好的约束进化算法在进化过程中的所表现出的相关性,有助于我们预估算法的有效决策子集。例如,在处理一个约束优化问题时,如果在目标优化过程中解的约束违反程度值显著减少,而在约束违反程度值最小化阶段解的目标值有所下降,这便表明通过目标优化可以实现约束违反程度值的最小化,从而帮助算法接近目标函数值较小的可行域。因此,有效决策子集可以估计在无约束最优解的邻域范围内。基于此,更多的评估资源便可以分配到目标优化上,以提高算法效率。本研究动机如下: (1) 通过衡量目标与约束之间的相关性来反映目标优化和约束违约最小化的同步优化性能;(2) 基于相关性动态确定有效决策子集,从而利用不同偏好的评估次数分配方案来精准求解不同类型的 COPs。 二、目标与约束之间的相关性分析 针对不同类型的约束优化问题,智能算法研究中心的研究人员提出了基于相关性的动态适应度评估分配的约束进化优化框架(Correlation-based Dynamic Allocation Scheme of Fitness Evaluations for Constrained Evolutionary Optimization)[2]。该框架通过不同问题目标和约束之间的相关性来确定进化算法在目标优化和约束处理上的分配方案。具体而言,如果目标优化阶段目标和约束之间的相关性比约束优化阶段相关性更强,算法则将自适应选择目标偏好比较标准来搜索目标较优区域,实现算法在目标优化上的算力分配。反之,若约束优化中的相关性表现更佳,则将选择约束偏好比较准则来分配算力。该研究工作目前已在国际顶级期刊IEEE Transactions on Evolutionary Computation发表。 该研究提出了基于相关性的动态算力分配方案(DAS)的约束进化算法,其主要思想是利用算法在目标优化和约束处理下目标函数值和约束违反程度值的共同趋势来反映目标优化或约束处理是否有利于搜索最优解,从而估计不同问题的有效决策子集。如图2所示。该方法通过分析目标与约束之间的共同下降趋势,衡量目标和约束之间和谐、冲突和独立相关性。考虑到不同算力分配方案下的采样数据一般不同,该研究分别利用目标偏好和约束偏好的分配方案来衡量相关性,从而获得基于目标和基于约束的相关性(定义如下)。
图2 基本思路 定义1:基于目标的相关性:给定,,,且,
定义2:基于约束的相关性:给定,,,且,
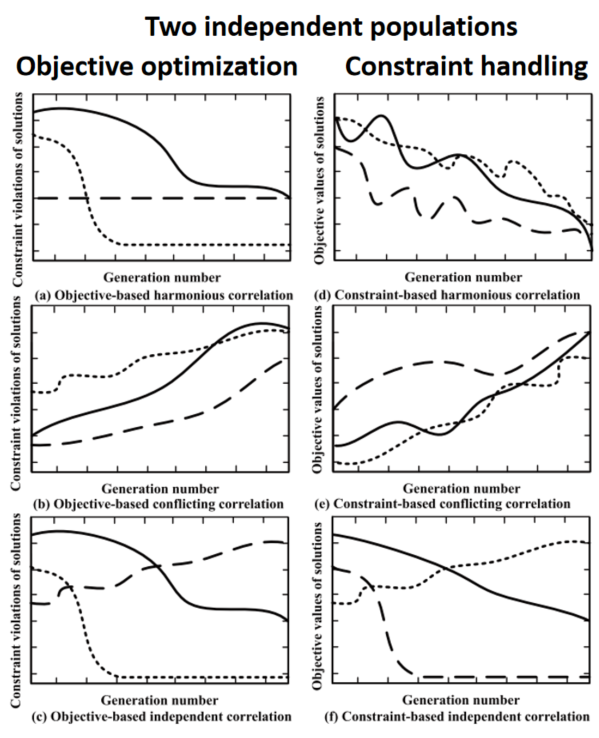
定义1中表示在基于目标的相关性的衡量过程中,种群目标函数值随着迭代进程下降。鉴于初始代和末代的评估结果反映了整个相关性衡量过程中目标和约束的重要变化趋势,本研究选择这两个数据点进行分析,以便更直接地观察和解释整个过程中的关键变动。采样数据的分析算法如算法1所示。具体来说,如果种群中所有个体在末代的约束违反程度值相较于初始代都有下降,则基于目标的相关性是和谐的(Algorithm 1,第8-9行)。在这种情况下,目标和约束具有共同的下降趋势 (见图3(a))。如果目标和约束没有共同的下降趋势 (见图3 (b)),即所有解其末代的约束违反程度值相较于初始代的约束违反程度值都增大 (第10-11行),其相关性是冲突的。只有当种群中一部分解的约束违反程度值呈上升趋势而其他解的约束违反程度值呈下降趋势时,相关性才是独立的(Algorithm 1,第12行)。类似地,确保了在衡量基于约束的相关性时约束违反程度值呈下降趋势,或保持不变。基于此,本文利用目标函数值的相应趋势来衡量基于约束的相关性(具体见图3(d-f))。
图3 相关性变化趋势
三、基于相关性比较的有效决策子集估计策略 该研究利用基于目标和约束的相关性来判断约束违反程度最小化和目标优化是否有助于搜索最优解,从而估计问题的有效决策子集。和谐关系越强,表示目标优化和约束违反程度最小化的同步效果越好。因此,本文根据两类相关性及其强度来估计算法的有效决策子集,并以此确定算力分配方案。具体地,本文假设: (1) 如果基于目标的相关性强于基于约束的相关性,则有效决策子集在无约束最优解邻域范围内。在这种情况下,算法应该将更多的评估次数分配给目标优化以逼近最优解; (2) 如果基于约束的相关性强于基于目标的相关性,则有效决策子集在解的搜索路径中约束违反程度较小的解的邻域。算法应将更多的评估次数分配给约束违反程度最小化以搜索最优解。 本文利用基于目标偏好和基于约束偏好进化算法在相关性衡量过程中的算法性能来衡量相关性强度。然而,考虑到基于两类偏好比较准则的算法分别专注搜索具有较小约束违反程度值和较小目标值的解,这些解之间可能不会被帕累托支配[3],且考虑到基于约束(目标)的相关性是通过目标函数值(约束违反程度值)在迭代中的变化趋势来衡量的,本文使用相关性衡量过程中解的目标函数值(约束违反程度值)来衡量基于约束(目标)的相关性强度。具体而言,本文将基于约束偏好进化算法获得的解的目标值与基于目标偏好进化算法获得的解的目标值进行比较,以此衡量基于约束的相关性强度。同样,本文通过比较解的约束违反程度值来衡量基于目标的相关性强度。 相关性强度比较结果分为三种,即基于目标的相关性强于、弱于和等于基于约束的相关性。在满足以下任一条件时,该研究认为基于目标的相关性更强。 条件1:基于目标偏好的算法比基于约束偏好的算法更有利于检测可行区域。条件2:基于约束偏好的算法和基于目标偏好的算法找到的解的约束违反程度差异值比目标函数值的差异更接近。 类似地,基于约束的相关性更强在满足以下任一条件时发生。 条件1:基于约束偏好的算法比基于目标偏好的算法更有利于找到目标值较小的解。 条件2:基于约束偏好的算法和基于目标偏好的算法找到的解的目标函数值差异比约束违反程度值的差异更接近。 本研究认为,当基于目标的相关性强度强于基于约束的相关性时,该问题的有效决策子集在无约束最优解的邻域,大部分的算力应该用于目标函数的优化,否则更多的算力应该用于约束处理。 四、基于动态评估次数分配的微搜索约束优化算法 该研究假设目标和约束之间的相关性可以帮助算法判断无约束最优解与最优解的接近程度。利用目标和约束之间的相关性强度评估方法,以确定不同约束优化问题的有效决策子集。在此基础上设计算力分配方案,即不同偏好的约束处理技术,用以实现有效决策子集上的算力分配。最后,将基于相关性的动态算力分配方案与其他算法进行集成,实现问题求解。
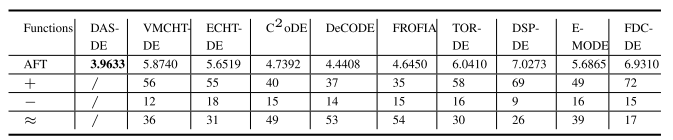
图4 微搜索框架 五、基于动态评估次数分配的微搜索约束优化算法 如图5所示,在104个不同相关性的测试函数中,基于相关性的动态算力分配方案(DAS)的优化算法35-72个测试问题上的表现都显著优于进化计算领域主流的基于目标偏好、基于约束偏好、基于非偏好的约束优化算法。实验结果验证了所提基于相关性的动态算力分配方案对约束进化算法求解不同约束优化问题具有积极影响。
图5 DAS-DE与其他基于EAs的分配方案对比 考虑到有效决策子集上的评估次数分配是通过不同的约束处理技术 (基于不同偏好的比较准则) 来辅助算法实现的,该研究利用不同偏好的比较准则 (见表2-1) 在不同相关性问题上的实验结果来验证算法估计的有效决策子集的准确性。具体而言,该研究对比了将基于相关性选择的不同偏好比较准则的算法与仅基于单一比较准则的四个算法,包括完全目标偏好比较准则(OP-C)、目标偏好比较准则 (OP)、完全约束偏好比较准则(CP-C)、约束偏好比较准则(CP) 的算法,基于相关性选择 CP-C和 OP-C 的比较准则的算法,以及基于相关性选择 CP和 OP的比较准则的算法进行对比。对比结果用以验证本文所提的DAS-DE算法及其搜索的有效决策子集的准确性。结果表明,所提算法在寻找具有较小目标值的可行解方面显著优于DAS-DE、OP-C-DE、OP-DE、 CP-C-DE、CP-DE、DAS-C-DE 和 DAS-P-DE。结果验证了由相关性选择的四个不同偏好的比较准则有助于精准地搜索最优解。
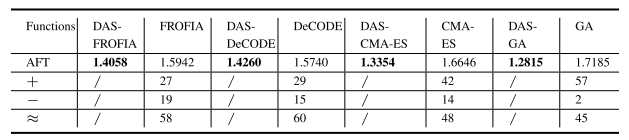
图6 有效决策子集验证结果 此外,该研究进一步验证了所提DAS在不同算法框架下的性能, 包括进化算法(如GA和CMA-ES) 和约束进化算法 (如FROFIA 和 DeCODE) 。如图7所示,基于相关性的动态算力分配方案显著增强了传统无约束进化框架和约束进化框架在解决约束优化问题时的性能。DAS使无约束进化算法和约束进化算法在解决不同相关性问题方面更具竞争力。这一结果证实了该研究所提出的动态算力分配方案(DAS)对不同进化算法的积极作用。
图7 DAS 在不同进化算法的实验效果 参考文献
总编:黄翰 责任编辑:雷墨鹥兮 文字:徐粤婷、邓淇 图片:徐粤婷 校稿:陈嘉慧 时间:2024年12月24日 |