微波滤波器作为信号频域分析中的重要器件，其精准度会直接影响信号处理的质量。器件中多个元件的参数设置会对微波滤波器的准确度产生决定性的影响。因此，每个微波滤波器在出厂前都需要接受元件参数调整以满足行业标准。调参任务通常由技术员人工调节微波滤波器上的螺母并观察矢量网络分析仪显示的散射数据变化是否满足标准（如图1所示）来完成。为降本增效，企业希望实现滤波器调参过程自动化。
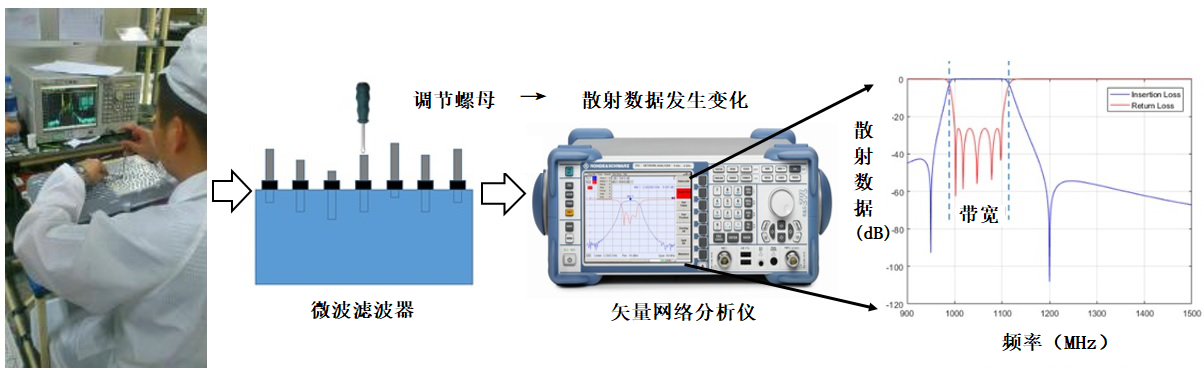
图1 微波滤波器的人工调参过程
根据滤波过程的机理，微波滤波器的调参过程常被建模为提取耦合矩阵的过程。当前主要有两大类求解滤波器调参问题的方法：一是解析法，通过构造数值多项式对耦合矩阵的提取进行分析，但其计算复杂度很高，几乎无法求解复杂的耦合矩阵提取问题；二是智能优化算法，通过在决策空间随机搜索的方式直接处理解析法难以求解的复杂问题，但在自动调参算法性能、耦合矩阵提取精度、调参误差等方面还有提升空间。
为了提升滤波器自动调参算法性能、降低调参误差，智能算法研究中心的研究人员将微波滤波器的实际耦合矩阵提取过程建模为一个大规模耦合矩阵优化问题，提出了基于耦合矩阵优化的目标空间分组微搜索算法来求解该问题。该算法通过对问题目标空间决策集进行分组，将原问题决策集转化为微小规模的有效决策子集，然后依次在每个有效决策子集内进行微搜索操作。这不仅避免算法将搜索算力部署到无效空间，还使算法在每个分组内有针对性地展开搜索，从而节省了搜索算力，提高了算法性能。目前，该研究工作已发表在人工智能领域的国际顶级学术期刊IEEE Transactions on Cybernetics（JCR一区，影响因子19.118）上。
一、抽丝剥茧：基于耦合矩阵分组优化的微搜索数学模型
微波滤波器的自动调参过程如图2所示。因为每个微波滤波器的耦合矩阵各异，所以第一步是提取微波滤波器实际耦合系数的耦合矩阵。接着，将实际耦合矩阵与最优耦合矩阵转换的散射数据进行比较，根据二者误差计算下一次调参的方向及范围。之后不断重复此过程，直到实际耦合矩阵与最优耦合矩阵转换的散射数据相同时，就可以得到该滤波器的最适参数集，完成自动调参。
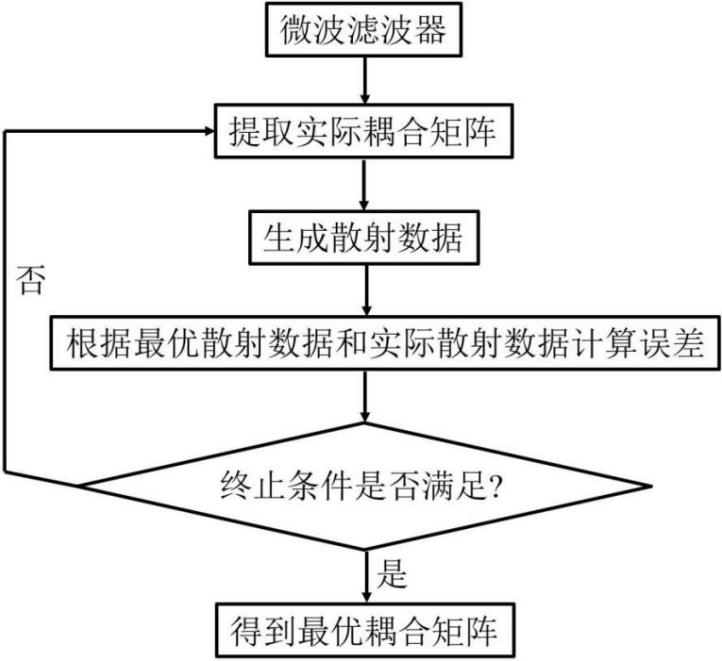
图2 微波滤波器自动调参流程图
以下是自动调参流程中耦合矩阵提取和误差最小化参数调整过程的详细描述：
耦合矩阵提取
以图3所示两端口微波滤波器的通用原型网络为例，表示微波滤波器中谐振器的数量，、和是微波滤波器的基本电路元件。表示第个和第个谐振器之间的耦合系数。这些耦合系数组成的耦合矩阵（公式(1)）反映了谐振器之间复杂的耦合关系。
(1)
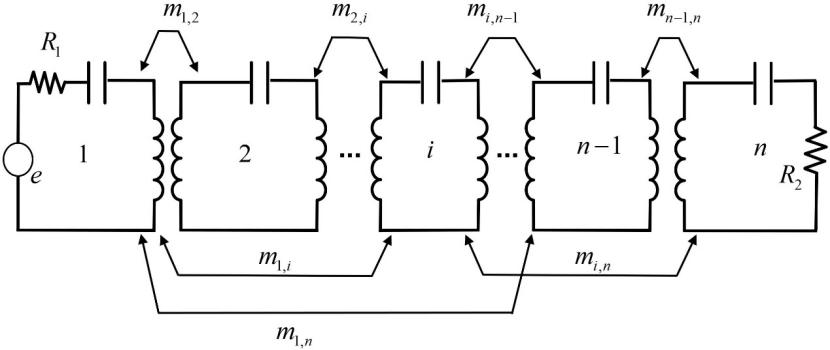
图3 两端口微波滤波器内部电路的通用原型网络
为降低直接求解复杂耦合矩阵的难度，根据其对称阵的特点，研究人员将矩阵上三角区的元素抽象为该矩阵的特征。编码过程如图4所示，从左到右顺序扫描每列中的元素，将耦合矩阵映射到一个向量。这种编码方式降低了原问题搜索空间的维度，缩小了无效决策集的规模，为后续算法规避了部分重复性操作。
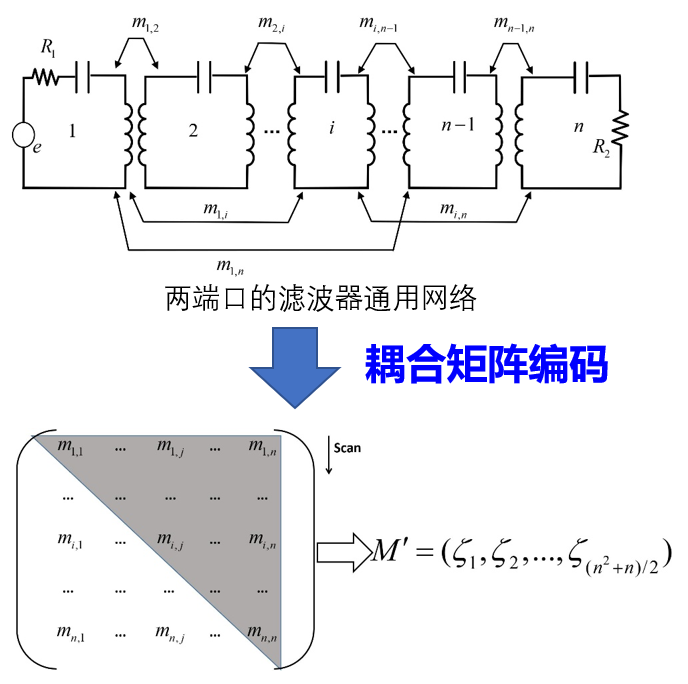
图4 耦合矩阵的编码过程
误差最小化参数调整
计算误差是所得耦合矩阵（候选解）与微波滤波器的真实耦合矩阵之间的差值。图5展示了候选解散射数据与真值的比较，两者误差越小，则说明候选解越接近真实值，该候选解在问题搜索空间中的分布越接近微小有效决策子集。
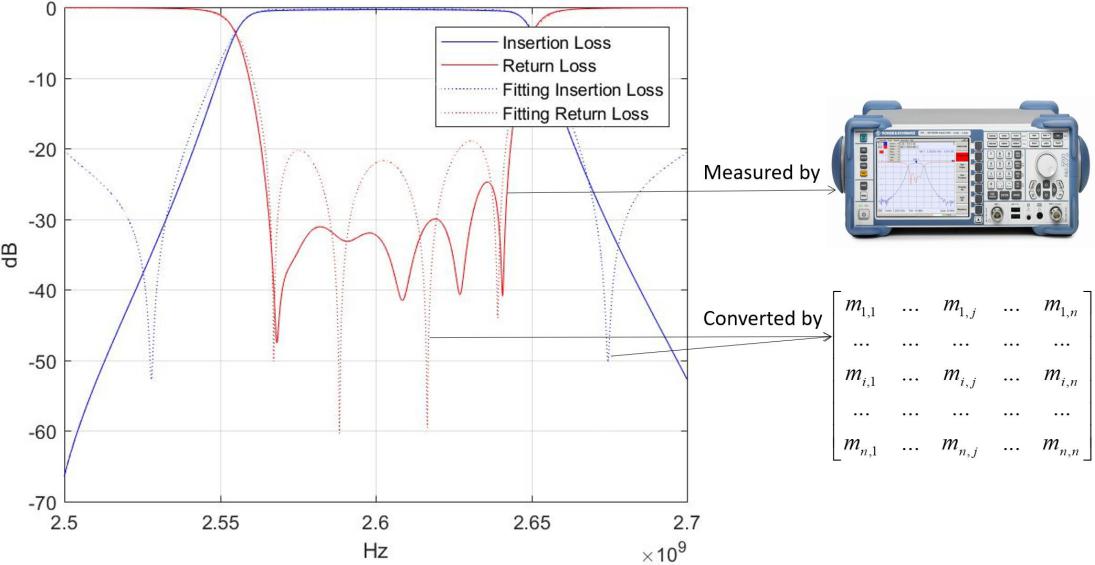
图5 工业滤波器调参过程中实际值与真实值的对比
因此，调参过程实际是一个求解误差最小化的大规模耦合矩阵问题的过程。为了降低问题求解的复杂度，研究人员建立了一个基于耦合矩阵分组优化的微搜索数学模型。该模型采用对决策变量分组的方式来缩小搜索空间的规模，最终得到公式(2)所示的基于耦合矩阵分组优化的数学模型。
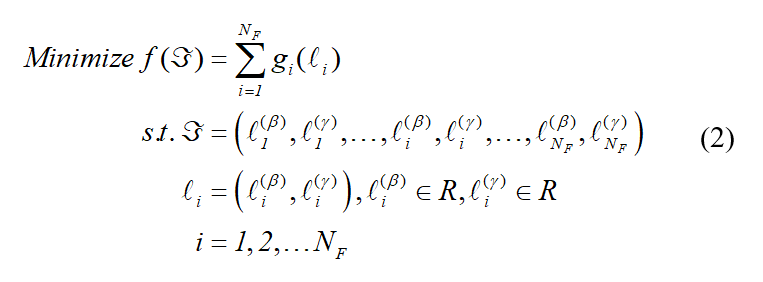
其中，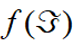
表示目标函数的计算误差，
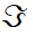表示频率区间内所有散射点的决策变量，表示频率区间上的第个决策变量。表示调节滤波器第个参数所产生的实际散射数据与真实散射数据之间的误差。和分别表示频率间隔上第个决策变量的插入损失和回波损失。表示固定频率区间内散射点的数量，表示插入损失，表示回波损失，表示实数的集合。
二、以简驭繁：基于耦合矩阵优化的目标空间分组微搜索算法
为求解上述大规模复杂耦合矩阵优化问题，研究人员设计了基于耦合矩阵优化的目标空间分组微搜索算法。该算法首先在目标空间上对搜索区域进行分组，再根据分组情况，有针对性地部署搜索资源，从而以较少的计算代价准确找到最优解。分组过程如图6所示。
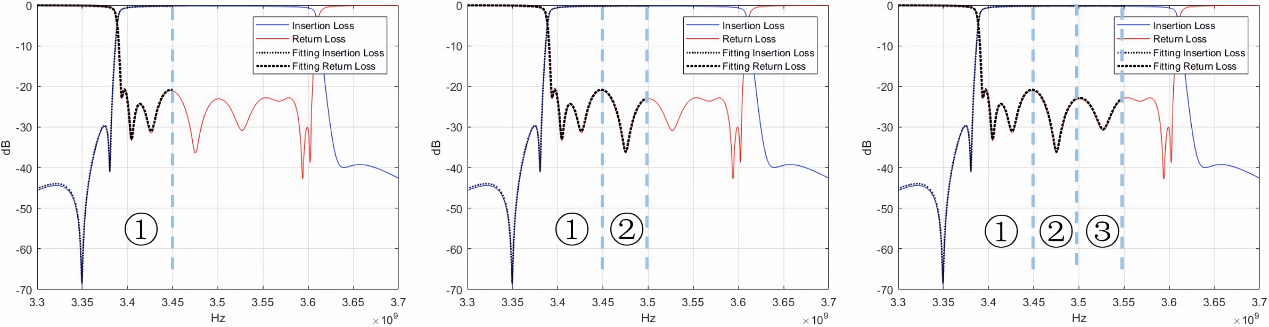
(a) (b) (c)
图6 目标空间动态分组优化的过程。其中，(a)为第一个子区间的拟合结果；(b)为第一个和第二个子区间的拟合结果；(c)为第一个、第二个和第三个子区间的拟合结果。黑色细虚线表示拟合插入损失，黑色粗虚线表示拟合回波损失，红色和蓝色实线表示真实散射数据。
为了在整个频率区间内搜索到真实散射数据，频率区间被划成多个子区间，分为多个小组。在优化的初始阶段（见图6(a)），使用第一个子区间的散射数据来评估耦合矩阵的精度。当初始阶段结束时，算法会找到当前最优耦合矩阵，从而保证第一组的拟合误差达到当前状态下的最小值。之后添加第二组散射数据来扩大评估范围（见图(b)）。该阶段将前一组的最优耦合矩阵作为当前搜索阶段的初始解，并利用历史信息引导算法向最优区域搜索。当第二阶段结束时，算法将会找到当前最优耦合矩阵，它能使第一和第二子区间的拟合误差达到最小。重复这个过程，直到算法完成对所有频率小组的搜索，此时算法将找到整个决策集上的最优耦合矩阵。
从该过程可以看出，基于耦合矩阵优化的目标空间分组微搜索算法在每个区间搜索时都会利用前一阶段的搜索信息，这些先验知识能指导算法对当前频域内更可能存在最优解的区域进行搜索，降低了算法在各阶段搜索的盲目性，节省了计算资源，提高了算法效率。
为了验证基于耦合矩阵分组优化的微搜索数学模型的通用性和可行性，研究人员在两端口微波滤波器上开展了九种不同测试用例的调参实验，图7展示了所提模型在测试用例上的调参结果。
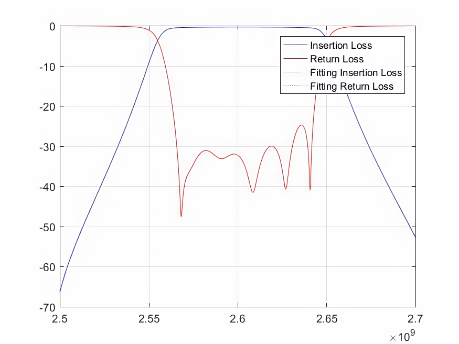
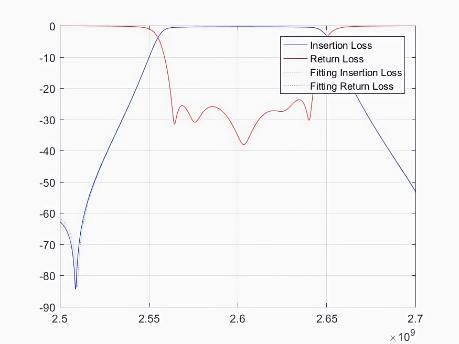
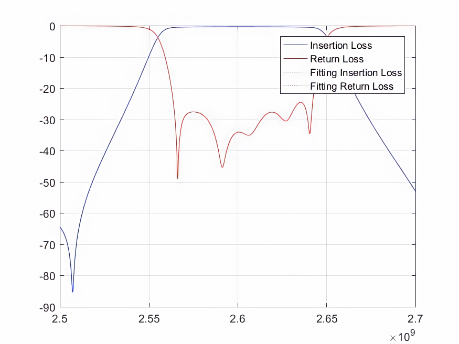
(a) (b) (c)
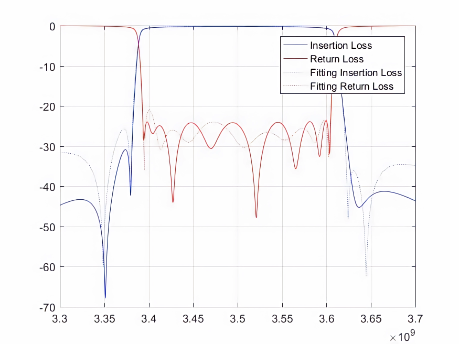
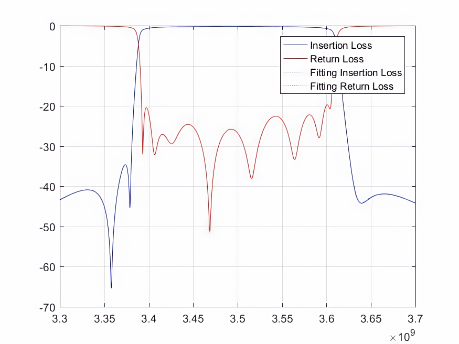
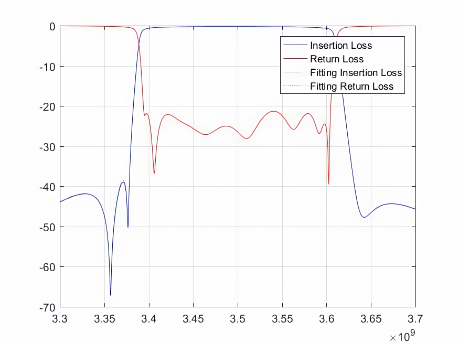
(d) (e) (f)
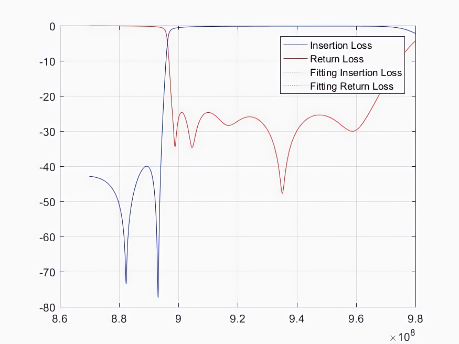
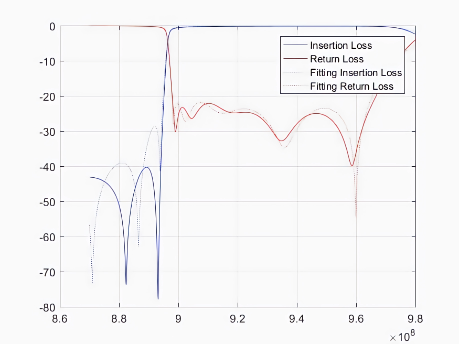
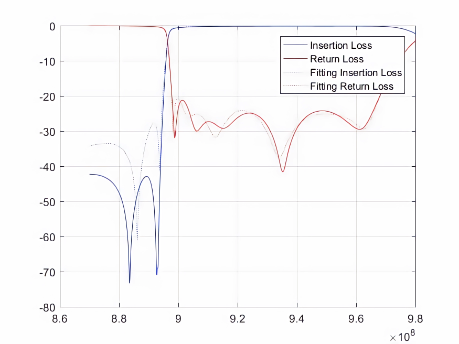
(g) (h) (i)
图7 频率区间的最优拟合可视化结果。其中，(a)-(c)为八阶微波滤波器测试用例1-3的拟合结果，(d)-(f)为九阶微波滤波器测试用例1-3的拟合结果，(g)-(i)为十阶微波滤波器测试用例1-3的拟合结果。
其中，红色和蓝色实线表示实际散射数据，虚线表示拟合的散射数据。实线和虚线的重合度越高就意味着自动微波滤波器的调优精度越高，也意味着该自动微波滤波器的质量越好。因此，该模型对于多版本的微波滤波器可行。
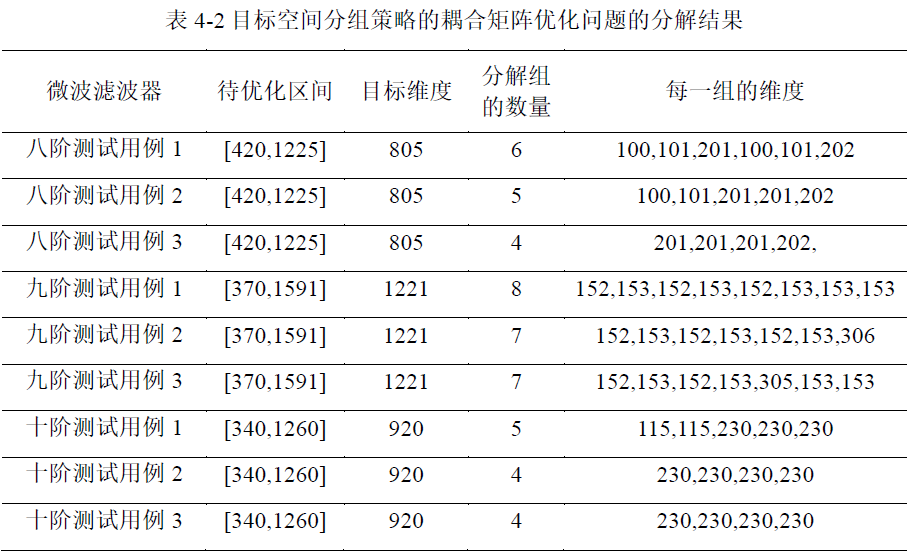
为对比目标空间分组策略的有效性，表1展示了本文所提分组策略在八阶微波滤波器、九阶微波滤波器和十阶微波滤波器上的分组结果。由表1可以看出，每个高维耦合矩阵优化问题都能分解为具有多个分组的低维优化子问题。这不仅意味着目标空间分组策略可以有效地分解具有强耦合性的复杂耦合矩阵优化问题，还表明频域子区间的相关性可以由相关系数矩阵来表示。
表1 目标空间分组策略的耦合矩阵优化问题分解结果
为了验证目标空间分组微搜索算法的有效性，研究人员以两端口微波滤波器的三个版本为测试案例，将本文所提算法与经典优化算法进行对比。表2展示了在九种测试案例上的对比结果。
表2 所提算法与目前典型优化算法在九种测试案例上的对比结果
MSA表示目标空间分组微搜索算法（Microscale Searching Algorithm）。
avg.mse表示拟合散射数据和最优散射数据的均方误差的均值。
sd.mse表示拟合散射数据和最优散射数据的均方误差的标准差。
+/=/- 分别表示所提目标空间分组微搜索算法的调优误差在Wilcoxon符号秩检验（）上显著高于、等于和低于对比算法。
粗体表示对比方法中性能最好的结果。
从误差平均值结果看，MSA均方误差的均值低于其他对比算法，因此，MSA在大多数用例上具有显著优势。从标准差角度看，虽然CMA-ES均方误差的标准差在九阶测试案例1、九阶测试案例2和十阶测试案例1上更小，CSO均方误差的标准差在十阶测试案例1上更小，但是MSA均方误差的标准差明显比二者稳定。
综上所述，基于耦合矩阵分组优化的微搜索数学模型能降低求解元素间具有强耦合关系的矩阵优化问题的复杂度，基于耦合矩阵优化的目标空间分组微搜索算法能够有针对性地在有效子空间进行搜索，减少多余和重复的搜索算力消耗，从而提高搜索效率并节省计算代价。实验结果表明，基于耦合矩阵分组优化的微搜索数学模型具有表征多版本微波滤波器调参问题的通用性，基于耦合矩阵优化的目标空间分组微搜索算法可以在计算代价相同的情况下提取出更加精确的耦合矩阵。其中，目标空间分组微搜索策略能够有效节省算力，能对多种型号的微波滤波器进行调参，且调参结果可以达到工业标准。
后续我们将进一步分析微波滤波器的物理模型，通过设计具有分布式计算的机器学习方法来提升自动微波滤波器调参的速度，为基于微波滤波器自动调参的工业机器人研发提供核心算法支撑。
参考文献
H. Huang, F. Feng, S. Huang, L. Chen and Z. Hao, “Microscale searching algorithm for coupling matrix optimization of automated microwave filter tuning,” IEEE Transactions on Cybernetics, doi: 10.1109/TCYB.2022.3166225.
H. Huang, S. Yang, X. Li and Z. Hao, “An embedded hamiltonian graph guided heuristic algorithm for two-echelon vehicle routing problem,” IEEE Transactions on Cybernetics, vol. 52, no. 7, pp. 5695-5707, 2022.
冯夫健,黄翰, 吴秋霞, 凌霄, 梁椅辉, 蔡昭权, “基于群体协同优化的高清图像前景遮罩提取算法,” 中国科学：信息科学, vol. 50, no. 3, pp. 424-437, 2020.
F. Feng, H. Huang and Y. Liang, “Graph-order optimization algorithm based on equal-in-space distance model for high-resolution image matting,” in 2021 IEEE 7th International Conference on Cloud Computing and Intelligent Systems (CCIS), 2021, pp. 122-127.
Z. Li, Q. Zhang, X. Lin and H. Zhen, “Fast covariance matrix adaptation for large-scale black-box optimization,” IEEE Transactions on Cybernetics, vol. 50, no. 5, pp. 2073-2083, 2020.
M. N. Omidvar, M. Yang, Y. Mei, X. Li and X. Yao, “DG2: A faster and more accurate differential grouping for large-scale black-box optimization,” IEEE Transactions on Evolutionary Computation, vol. 21, no. 6, pp. 929-942, 2017.
