
随着城市中的货运车辆越来越多,城市交通管理和环境保护的压力与日俱增。为了提高物流效率,减轻货物运输所带来的负面影响,多层城市物流系统应运而生。其中,双层物流系统是多层城市物流系统最简单的形式。在双层物流系统中,大型货车把货物从仓库运送到中转站(卫星),再由小型货车完成最后一段的货物运输。
不论是战略层面的城市物流系统规划,还是日常运作层面的车辆路径管理,双层车辆路径问题(Two-Echelon Vehicle Routing Problem, 2E-VRP)A. Schrijver, Combinatorial optimization: polyhedra and efficiency, vol. 24. Springer Science and Business Media, vol. 24, 2003.都是必须要解决的关键一环。双层车辆路径优化问题(Two-Echelon Vehicle Routing Problem, 2E-VRP)是一类NP难的组合优化问题A. Schrijver, Combinatorial optimization: polyhedra and efficiency, vol. 24. Springer Science and Business Media, vol. 24, 2003.。2E-VRP作为一个基本数学模型,现已应用于现代城市物流——通过中间配送设施(卫星)管理物流的配送。而由于NP-hard难度,2E-VRP在多项式计算时间内获得所有最优解是非常困难的。

现有的求解2E-VRP求解的方法多利用变邻域搜索等局部优化算子对卫星进行随机打开、移除、交换等操作,得到2E-VRP的局部最优解。然而,这些方法过分依赖局部信息和局部优化算子,忽略了2E-VRP最优路径具有无交叉点哈密尔顿路的特点。
微搜索是一种在微小范围内的有效的定向搜索方法,它能集中算力,在某个确定的方向或者范围内获得高质量的解。由于相对于2E-VRP完整的解集而言,具有嵌入式哈密尔顿子图结构的解集是一个微小的搜索范围,因此智能算法研究中心的研究人员基于微搜索假设,结合2E-VRP最优路径具有哈密尔顿图的特性,在全局范围内将2E-VRP的最优路径规划考虑为基于一个嵌入式哈密尔顿图的搜索过程,提出一个基于嵌入式哈密尔顿图的启发式算法(Embedded Hamiltonian Graph-guided Heuristic Algorithm, EHG-HA)H. Huang, S. Yang, X. Li*, and Z. Hao, “An Eembedded hHamiltonian gGraph gGuided hHeuristic aAlgorithm for tTwo-eEchelon vVehicle rRouting pProblem,” IEEE Transactions on Cybernetics, doi: 10.1109/TCYB.2021.3108597。该算法可以在不违反任何一个约束条件的情况下搜索出交叉点尽可能少的哈密尔顿路径,从而获得2E-VRP的高质量求解。目前,此项成果已经发表在智能优化领域的国际学术期刊IEEE Transactions on Cybernetics(JCR一区,影响因子11.448)上。下面我们将对该研究工作展开介绍。
的局限性是过分依赖局部信息和局部优化算子。这些方法利用变邻域搜索等局部优化算子对卫星进行随机打开、移除、交换等操作,得到2E-VRP的局部最优解。然而,现有的方法忽略了以无交叉点的哈密尔顿路径形式来构造2E-VRP路径的思想。基于这一观点,智能算法研究中心的研究人员将2E-VRP的最优路径规划考虑为一个嵌入式哈密顿图,提出一个基于嵌入式哈密尔顿图的启发式算法(Embedded Hamiltonian Graph guided Heuristic Algorithm, EHG-HA)H. Huang, S. Yang, X. Li*, and Z. Hao, “An Eembedded hHamiltonian gGraph gGuided hHeuristic aAlgorithm for tTwo-eEchelon vVehicle rRouting pProblem,” IEEE Transactions on Cybernetics, doi: 10.1109/TCYB.2021.3108597,在不违反任何一个约束条件的情况下,可以绘制出含有尽可能少交叉点的哈密尔顿路径,从而优化2E-VRP的解。嵌入式哈密尔顿图结构中搜索就是一种定向微小范围的搜索方式,简称:微搜索。目前,相关研究成果论文已经成功发表在智能优化领域的国际学术期刊IEEE Transactions on Cybernetics(JCR一区,影响因子11.448)上发表。下面我们将对本研究工作的相关成果展开介绍。

基于嵌入式哈密尔顿图的启发式算法(EHG-HA)流程如图1,主要包括三个阶段:初始化、卫星调整和路线重建。其中,我们主要在初始化机制和卫星调整机制上进行了创新。
下面,我们将重点介绍算法中初始化机制(Initialization Scheme based on an Embedded Hamiltonian Graph, ISEHG)和动态卫星调整机制(Dynamic Adjustment for Satellites, DAS)。
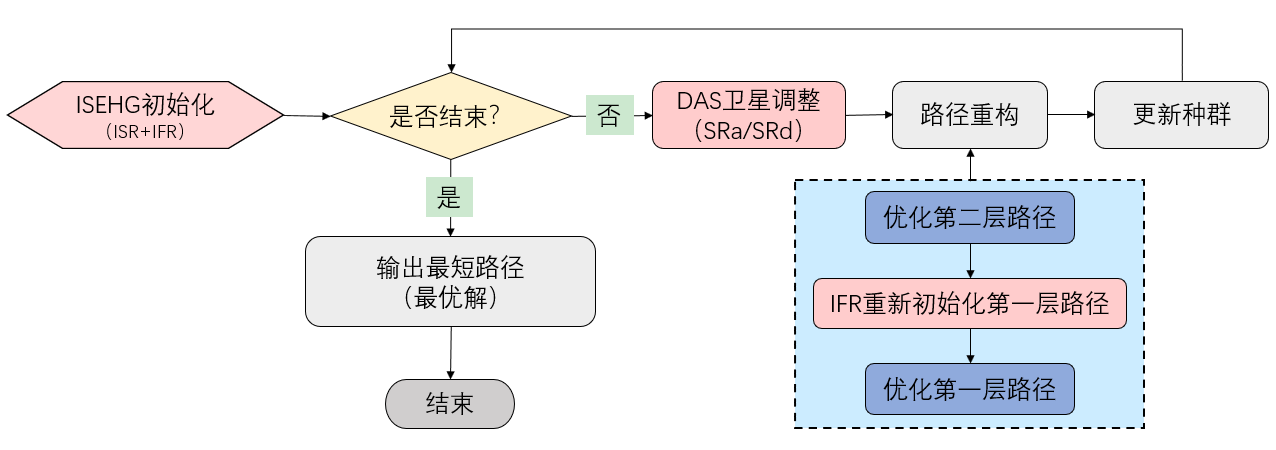
图1 EHG-HA算法的说明流程示例
初始化机制第一部分:初始化机制种“花”得“花”
嵌入式哈密尔顿图由嵌入式车辆路径组成,这些路径都是没有交叉点的哈密尔顿路径电路。如果将车辆段仓库和卫星视为两组不同的顶点,并且车辆的能力车载容量是无限的,则那么具有最优路径规划的2E-VRP图是一个嵌入式哈密尔顿图。基于以上理论,我们提出一个基于哈密尔顿图的初始化机制(Initialization Scheme based on an Embedded Hamiltonian Graph, ISEHG)(Initialization Scheme based on an Embedded Hamiltonian Graph, ISEHG)。图4展现了整个初始化2E-VRP解的过程。
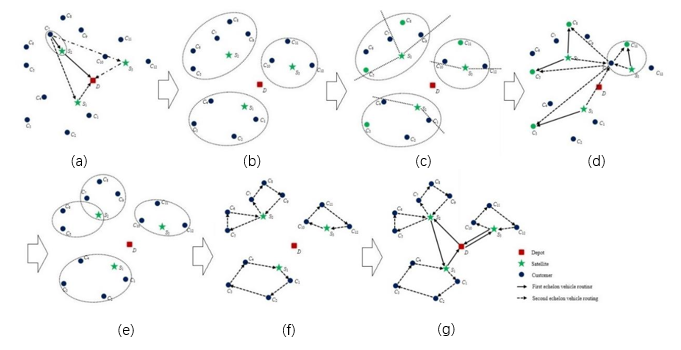
图2 ISEHG的说明示例。(a)为客户分配卫星,(b)根据所属卫星对客户分组,(c)根据角度对客户分组,(d)为每条路线选择每个最远的客户,(e)根据卫星和最远的客户重新分配剩余客户,(f)完成第二层路径的初始化,(g)完成第一层路径的初始化。
图2展现了整个初始化2E-VRP解的过程。因为最优解包含了嵌入式哈密尔顿图结构,所以采用微搜索方法所获得的解的质量显著较高。
由于2E-VRP有两层路径需要优化,因此,初始化机制通过微搜索构造嵌入式哈密尔顿图,主要分为两个阶段对2E-VRP的解进行初始化2E-VRP的解,所提出的ISEHG包含两种策略,分别初始化第二层级和第一层级路径,图23和图34分别给出了所提出的ISEHG包含的两种策略的伪代码。




图2 3 算法1初始化第二层级路径(ISR) 图3 4 算法2初始化第一层级路径(IFR)
图4展现了整个初始化2E-VRP解的过程。
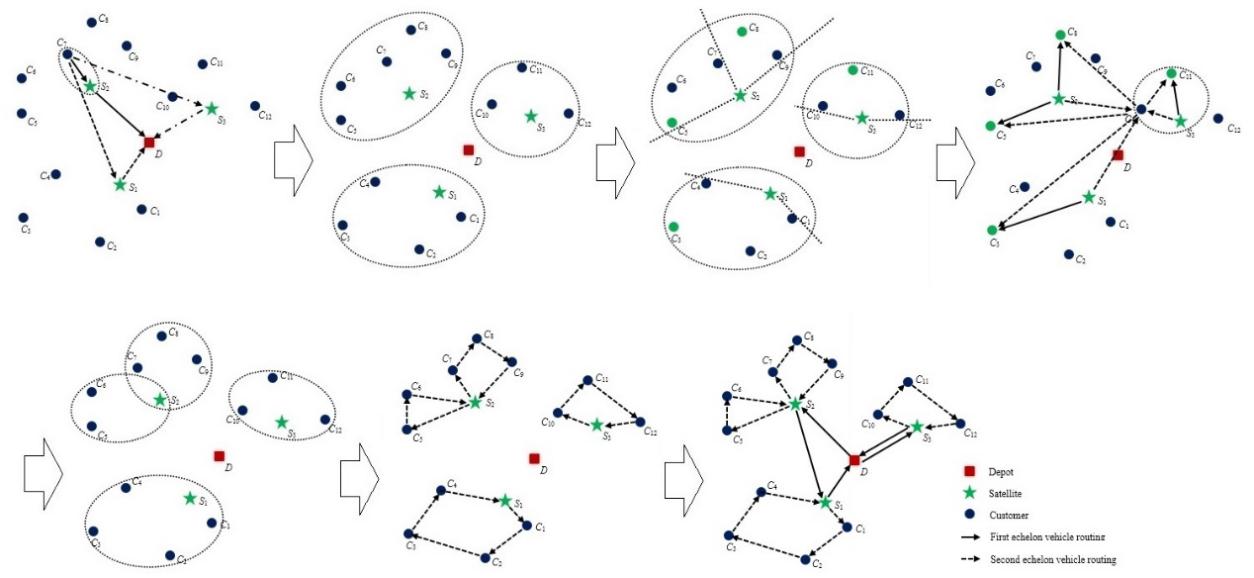
图4 初始化机制的说明示例,(a)为客户分配卫星,(b)根据所属卫星对客户分组,(c)根据角度对客户分组,(d)为每条路线选择每个最远的客户,(e)根据卫星和最远的客户重新分配剩余客户,(f)完成第二层级路径的初始化,(g)完成第一层级路径的初始化。
第二部分:动态卫星调整机制:“花”开不败
卫星在连接2E-VRP的两层路径中起着非常重要的作用。一旦一个卫星的状态发生变化,与同一个该卫星相连的客户和仓库必须被重新安排到其他卫星上。因此,原来的路径基本上被破坏了。当随机对卫星的状态进行改变(移除、打开、交换)时当随机对卫星的状态进行改变,即移除、打开和交换,路径中的交叉点数量可能会增加路径中的交叉点数量。由此,我们提出一个动态卫星调整机制(Dynamic Adjustment for Satellites, DAS)(Dynamic Adjustment for Satellites, DAS),旨在通过微搜索获得含有尽可能少交叉点尽可能少交叉点的路径。DAS与之前最大的不同就是保持嵌入式哈密尔顿图不变,即维持路径“花”的形态。
DAS主要由两个策略组成:卫星重排策略(Satellite Rearrangement, SRa)和卫星约简策略(Satellite Reduction, SRd)。
SRa策略先将移除所有二层级路径移除,再根据贪婪操作符选择卫星,将其重新插入路径中。SRa调整了第二层级路径连接的卫星,图5展示了其实现过程。
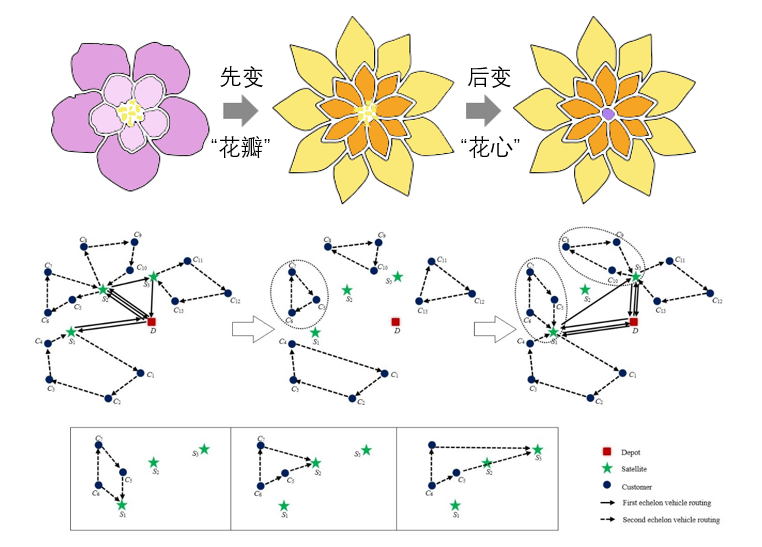
图5 SRa策略卫星调整的说明示例
SRd策略将容量最小的卫星的运输任务分配给插入成本偏差最小的卫星,根据第二层卫星的使用情况重新调整所有第一层级路径均根据第二层级卫星的使用情况重新调整,同时确保成本低于以前降低。SRd通过移除冗余的卫星来优化第一层路径连接的卫星,图6展示了其实现过程。
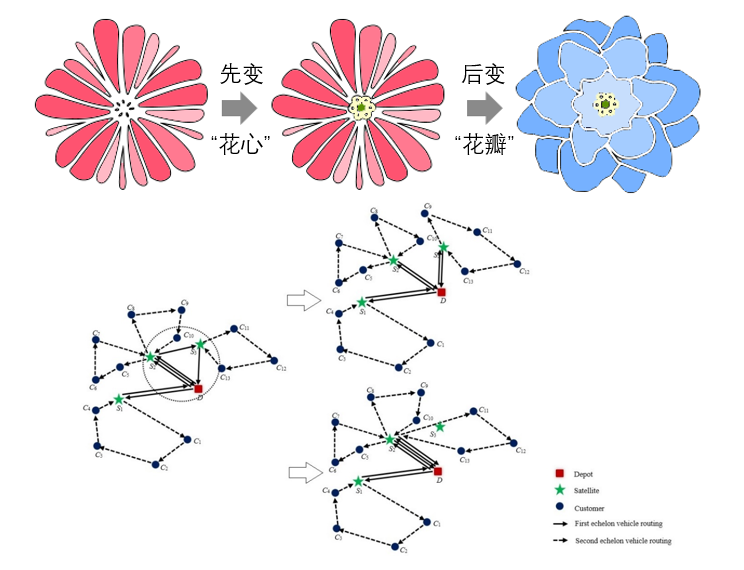
图6 SRd策略卫星调整的说明示例
为了验证EHG-HA算法对求解2E-VRP求解的有效性,智能算法研究中心搜集整理出了一个全面的2E-VRP测试集(下载地址:http://www2.scut.edu.cn/huanghan/kycg/list.htm)。该测试集的详细信息如表1所示。(下载地址:http://www2.scut.edu.cn/huanghan/kycg/list.htm)
表1 测试集的详细信息表
该测试集数据数量庞大,包含了集合测试集2-6中的207个测试用例,性能优秀,能有效检验2E-VRP相关算法的优劣。与此同时,这也是从2E-VRP问题被提出以来,包含问题数量最多的测试集。,可以说在全世界排名第一!

为了考察ISEHG初始化对2E-VRP求解的贡献,研究人员分别将它与五个初始化方法(NNMD. J. Rosenkrantz, R. E. Stearns, and P. M. Lewis, “An analysis of several heuristics for the traveling salesman problem,” in Fundamental Problems in Computing (S. S. Ravi S.S., ed.), Dordrecht: Springer, 2009.、CWG. Clarke and J. W. Wright, “Scheduling of vehicles from a central depot to a number of delivery points,” Operations Research, vol. 12, no. 4, pp. 568–581, 1964.、IM[5]、SAG. Clarke and J. W. Wright, “Scheduling of vehicles from a central depot to a number of delivery points,” Operations Research, vol. 12, no. 4, pp. 568–581, 1964.、SMJ. E. Beasley, “Route first-cCluster second methods for vehicle routing,” Omega, vol. 11, no. 4, pp. 403–408, 1983.)进行了比较。表2给出了所有初始化算法性能比较的统计数据结果。ISEHG 在所有实例上都明显优于NNM D. J. Rosenkrantz, R. E. Stearns, and P. M. Lewis, “An analysis of several heuristics for the traveling salesman problem,” in Fundamental Problems in Computing (S. S. Ravi S.S., ed.), Dordrecht: Springer, 2009.、SA G. Clarke and J. W. Wright, “Scheduling of vehicles from a central depot to a number of delivery points,” Operations Research, vol. 12, no. 4, pp. 568–581, 1964.和SM J. E. Beasley, “Route first-cCluster second methods for vehicle routing,” Omega, vol. 11, no. 4, pp. 403–408, 1983.。ISEHG,在194个实例上的表现明显优于CW G. Clarke and J. W. Wright, “Scheduling of vehicles from a central depot to a number of delivery points,” Operations Research, vol. 12, no. 4, pp. 568–581, 1964.,在13个实例上的表现差于 CW。
表2 初始化算法的性能比较结果

为调查本文提出的DAS机制是否有效,研究人员开发了不使用DAS的EHG-HA变体EHG-HA-DAS和添加了局部搜索算子的EHG-HA变体EHG-HA+LS。开发了EHG-HA-DAS作为不使用DAS的EHG-HA变体。表3总结了六种算法(EHG-HA、ALNSV. C. Hemmelmayr, J. F. Cordeau, and T. G. Crainic, “An adaptive large neighborhood search heuristic for two-echelon vehicle routing problems arising in city logistics,” Computers & Operations Research, vol. 39, no. 12, pp. 3215–3228, 2012.、LNS-2EU. Breunig, V. Schmid, R. F. Hartl, and T. Vidal, “A large neighbourhood based heuristic for two-echelon routing problems,” Computers & Operations Research, vol. 76, pp. 208–225, 2016.、GFEAX. Yan, H. Huang, Z. Hao, and J. Wang, “A graph-based fuzzy evolutionary algorithm for solving two-echelon vehicle routing problems,” IEEE Transactions on Evolutionary Computation, vol. 24, no. 1, pp. 129–141, 2020.、EHG-HA-DAS、EHG-HA+LS)在207个测试用例上的性能比较结果。EHG-HA的表现明显优于ALNS V. C. Hemmelmayr, J. F. Cordeau, and T. G. Crainic, “An adaptive large neighborhood search heuristic for two-echelon vehicle routing problems arising in city logistics,” Computers & Operations Research, vol. 39, no. 12, pp. 3215–3228, 2012.、LNS-2E U. Breunig, V. Schmid, R. F. Hartl, and T. Vidal, “A large neighbourhood based heuristic for two-echelon routing problems,” Computers & Operations Research, vol. 76, pp. 208–225, 2016.和GFEA X. Yan, H. Huang, Z. Hao, and J. Wang, “A graph-based fuzzy evolutionary algorithm for solving two-echelon vehicle routing problems,” IEEE Transactions on Evolutionary Computation, vol. 24, no. 1, pp. 129–141, 2020.。此外,EHG-HA在60个实例上的表现显著优于EHG-HA- DAS,在36个实例上的表现显著低于EHG-HA- DAS。实证结果表明,DAS机制对于EHG-HA是不可或缺的。
表3 六个算法的性能比较结果

图7显示了使用六种算法求解2E-VRP构造的嵌入式哈密尔顿图路径交叉点个数的统计结果。与其他五种算法相比, EHG-HA算法在大多数情况下都能获得交叉点口最少的路径。随着测试用例规模的增加,路线规划交叉点增加。总的来说,由该算法生成的路线中的交叉点口数量少于其他对比算法获得的交叉点口数量。
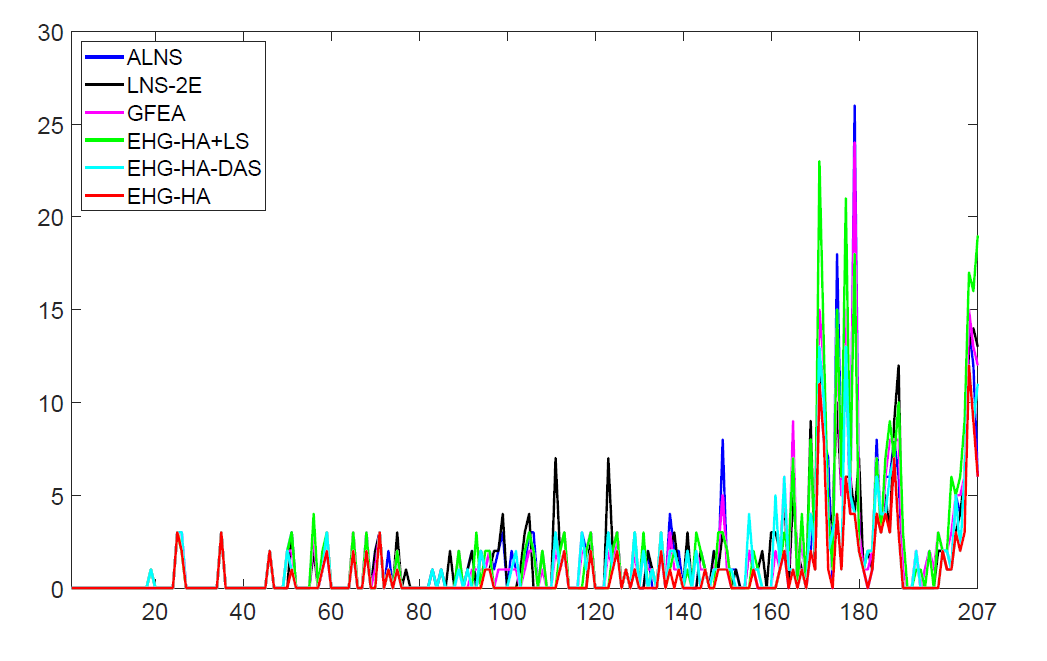
图7 六种算法求解207个实例的路径交叉点个数统计,x轴中的1到207表示实例的序列号,其中1-30、31-54、55-162、163-180和181-207分别表示测试集集合2、3、4、5和6的实例,y轴表示交点交叉点的数量。
此外,图8给出了EHG-HA求解测试集5的6个测试用例的路径结构图,进一步证明了EHG-HA在大部分实例中可以比其它对比比较算法取得更少的路径交叉点个数。,基于嵌入式哈密尔顿图的微搜索“花”式求解是十分有效的。
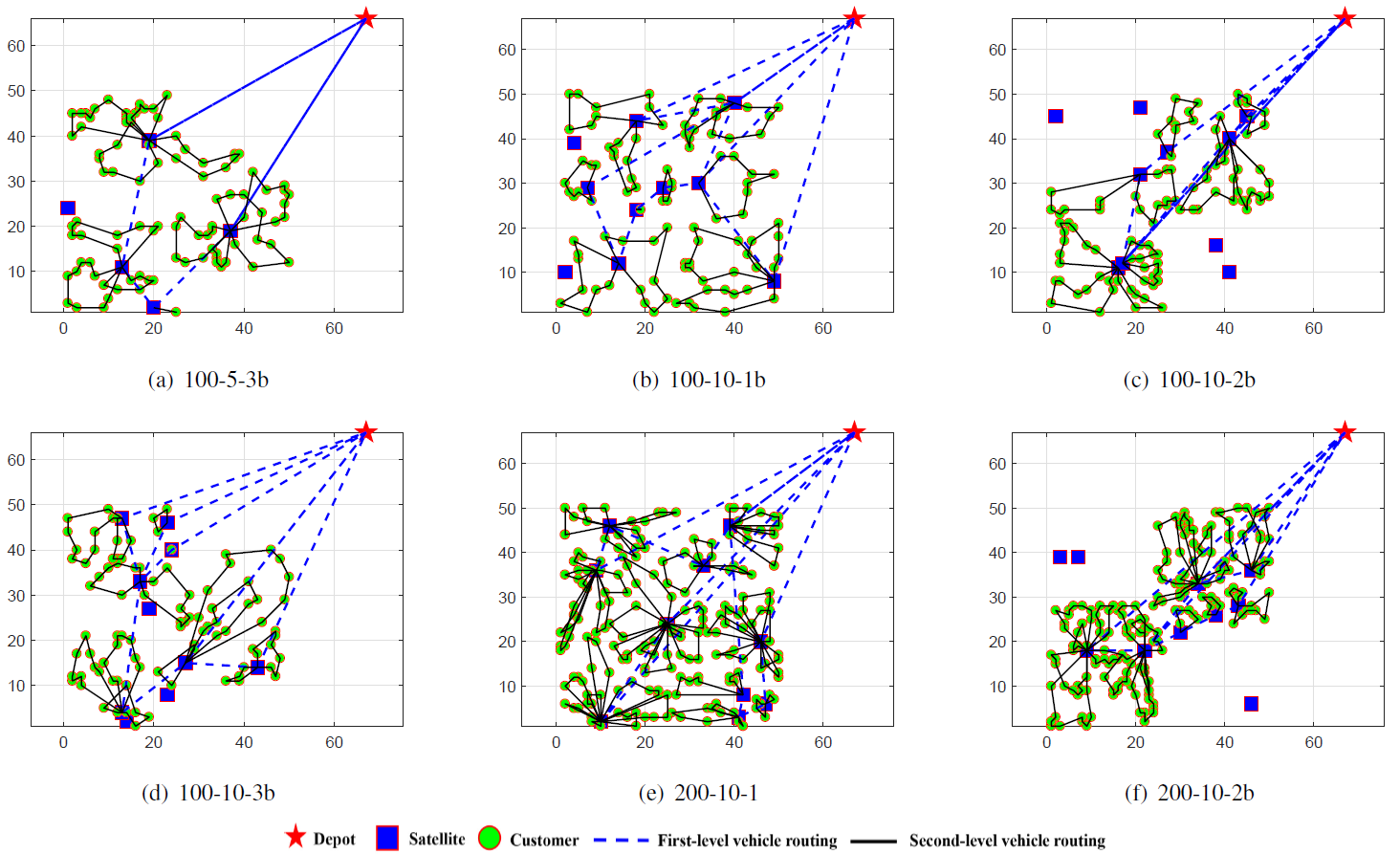
图8 EHG-HA求解测试集5的6个测试用例的路径结构图
总体而言,通过在嵌入式哈密尔顿图中进行微搜索,EHG-HA在求解大规模2E-VRP实例方面取得了显著的进步,在性能上明显优于ALNS、LNS-2E、GFEA等现有的高水平算法。微搜索方法的优势在EHG-HA上展露无遗!
综上所述,本文提出的EHG-HA算法在求解2E-VRP的性能与ALNS、LNS-2E和GFEA相当,甚至比这三种算法更好。基于嵌入哈密顿图的指导思想,EHG-HA在求解大规模2E-VRP实例方面取得了显著的进步。总体而言,在由于嵌入式哈密顿图中进行微搜索的引导,EHG-HA算法求解2E-VRP的性能显著优于其他比较算法。微搜索初试锋芒,就成为当前最高性能的2E-VRP问题求解算法(没有之一!)。


考虑到基于种群的启发式方法的多样性可以提高元启发式方法的性能,接下来的研究将致力于开发EHG-HA的多样性改进策略。未来,我们将研究如何有效划分搜索空间的有效决策子集,进一步挖掘子图结构,缩小搜索空间,使算法能够在有限的评估次数内快速得到问题的可行解。未来,我们将
研究多目标2E-VRP,以验证2E-VRP作为嵌入哈密顿图的路径规划的可扩展性。
考虑到基于种群的启发式方法的多样性可以提高元启发式方法的性能,接下来的研究将致力于开发EHG-HA的多样性改进策略。
参考文献
A. Schrijver, Combinatorial optimization: polyhedra and efficiency, vol. 24. Springer Science and Business Media, vol. 24, 2003.
H. Huang, S. Yang, X. Li*, and Z. Hao, “An Eembedded hHamiltonian gGraph gGuided hHeuristic aAlgorithm for tTwo-eEchelon vVehicle rRouting pProblem,” IEEE Transactions on Cybernetics, doi: 10.1109/TCYB.2021.3108597.
D. J. Rosenkrantz, R. E. Stearns, and P. M. Lewis, “An analysis of several heuristics for the traveling salesman problem,” in Fundamental Problems in Computing (S. S. Ravi S.S., ed.), Dordrecht: Springer, 2009.SIAM Journal on Computing, vol. 6, no. 3, pp. 563-581, 1977.
G. Clarke and J. W. Wright, “Scheduling of vehicles from a central depot to a number of delivery points,” Operations Research, vol. 12, no. 4, pp. 568–581, 1964.
R. H. Mole and S. R. Jameson, “A sequential route-building algorithm employing a generalised savings criterion,” Journal of the Operational Research Society, vol. 27, no. 2, pp. 503–511, 1976.
B. E. Gillett and L. R. Miller, “A heuristic algorithm for the vehicle dispatch problem,” Operations Research, vol. 22, no. 2, pp. 340–349, 1974.
J. E. Beasley, “Route first-cCluster second methods for vehicle routing,” Omega, vol. 11, no. 4, pp. 403–408, 1983.
G. Clarke and J. W. Wright, “Scheduling of vehicles from a central depot to a number of delivery points,” Operations Research, vol. 12, no. 4, pp. 568–581, 1964.
V. C. Hemmelmayr, J. F. Cordeau, and T. G. Crainic, “An adaptive large neighborhood search heuristic for two-echelon vehicle routing problems arising in city logistics,” Computers & Operations Research, vol. 39, no. 12, pp. 3215–3228, 2012.
U. Breunig, V. Schmid, R. F. Hartl, and T. Vidal, “A large neighbourhood based heuristic for two-echelon routing problems,” Computers & Operations Research, vol. 76, pp. 208–225, 2016.
X. Yan, H. Huang, Z. Hao, and J. Wang, “A graph-based fuzzy evolutionary algorithm for solving two-echelon vehicle routing problems,” IEEE Transactions on Evolutionary Computation, vol. 24, no. 1, pp. 129–141, 2020.
总编:黄翰
责任编辑:袁中锦
文字:杨舒玲、梁靖欣
图片:杨舒玲、梁靖欣
校稿:何莉怡
时间:2021年11月30日


