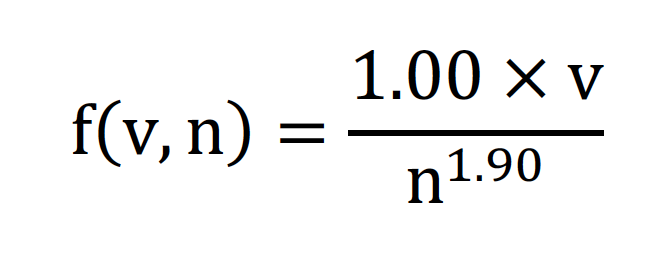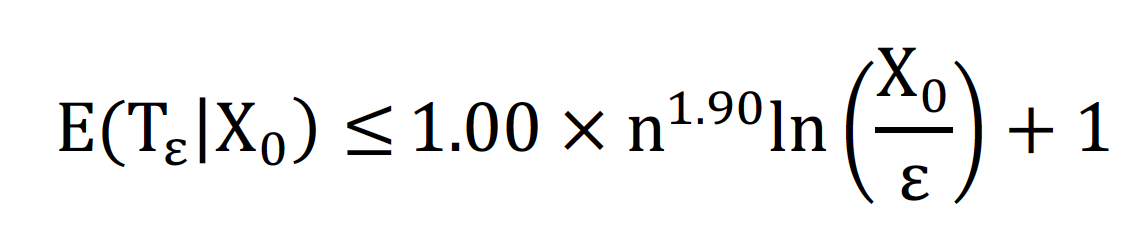| 好消息!以后会编程就能分析进化算法的时间复杂度了 |
| 发布时间: 2019-10-24 浏览次数: 512 |
|
随着人工智能浪潮的迅猛发展,进化算法在诸多实际应用领域中都取得了显著的效果。在之前的推文中,我们介绍了进化算法常被用于求解高维多目标优化、软件测试用例自动生成以及红外行人抠图等不同领域的问题,也介绍了在实际应用中,进化算法被广泛用于双层次车辆路径规划、多个城市物流路线规划解决方案以及一些大型港口的资源调度分配问题解决等应用上,如图一进化算法的应用场景示例所示。
图一 进化算法的应用场景示例 尽管进化算法已被广泛地应用于现实工业问题,但该类算法的理论分析却相对滞后,例如,时间复杂度的估算就是困扰了进化计算领域五十多年的难题。而计算时间复杂度是算法应用时所必需的名片,因此有必要对实际应用中的进化算法进行时间复杂度分析。 由于进化算法的随机性以及搜索算子的复杂性,计算时间复杂度的分析过程往往繁琐而艰难。因此大部分理论工作只能针对简化后的进化算法进行分析,例如在每次迭代中仅产生一个新解的(1+1) EA [2]。然而,简化后的算法性能有所下降,不适用于求解实际问题,因此常被称为“玩具模型”。据统计,在我们查到的30余篇讨论(1+1)EA的论文中,尚未发现将(1+1)EA用于解决实际优化问题的工作[3,4]。另外,少数几篇论文讨论了多种群EA [5,6],被讨论的算法同样很少用于实际应用,其现状正如下图二漫画所示。
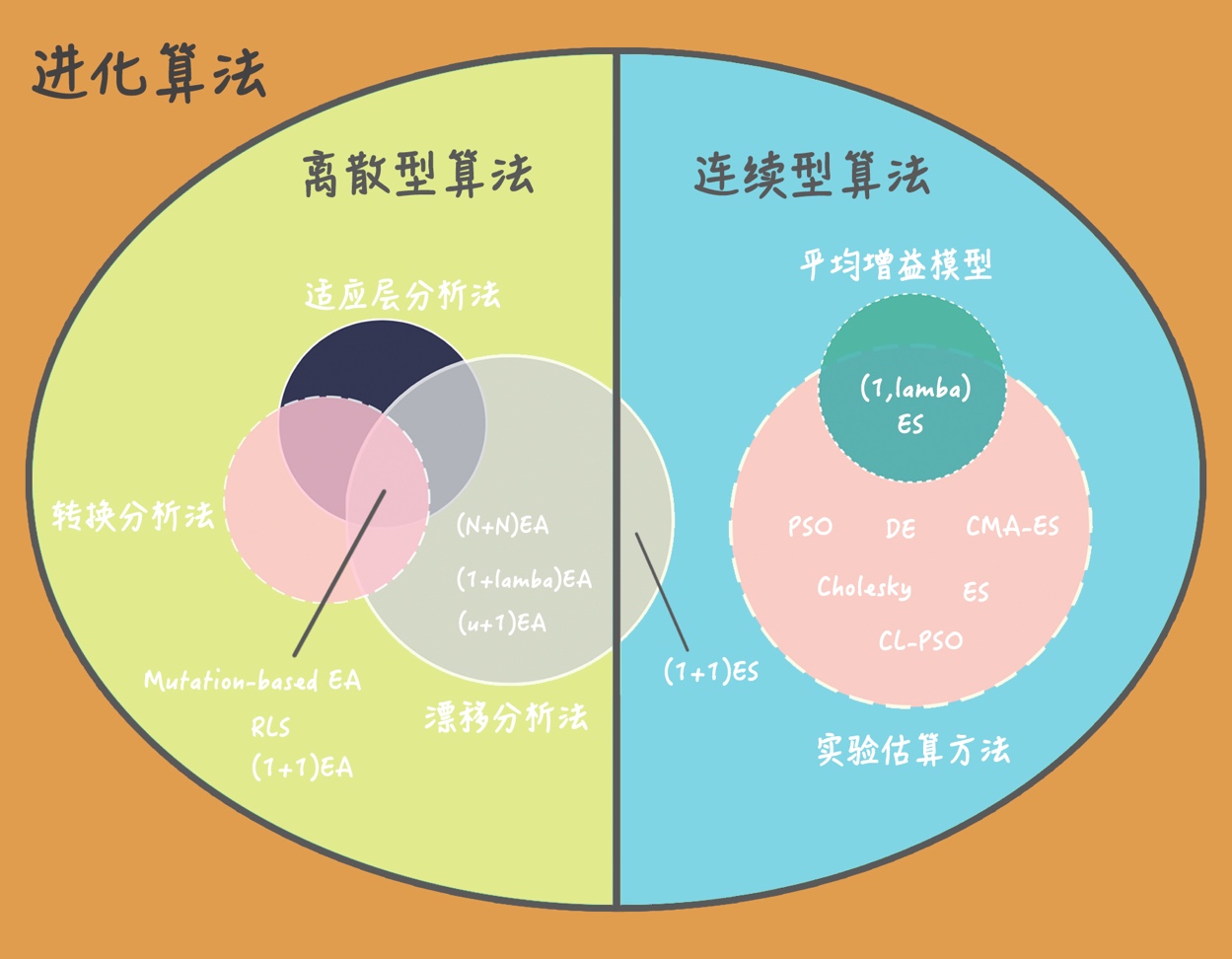
图二 进化算法理论分析的现状 即便是经过简化后的“玩具”算法,也往往需要十几页的数学推导才能得到粗略的分析结果,而实用性进化算法的分析难度更高。不过近期我们的研究成果将有望解决这一难题,届时采用我们的方法即可高效快捷地得出计算时间复杂度,并且它几乎适用于所有的进化算法。不仅如此,经过我们的验证和理论分析,最后分析得到的结果与实际结果精度相当。从此对进化算法进行计算时间复杂度的分析不再是空中楼阁。 基于上述如何去分析计算时间复杂度这个问题,我们提出了一种基于平均增益模型的连续型进化算法时间复杂度估算方法[1]。如下图三各进化算法分析策略适用范围的韦恩图所示,本项工作提出的估算方法可以分析大部分的连续型实用进化算法,实际应用更为广泛。目前,该研究成果已成功发表在进化计算领域顶级国际学术期刊IEEE Transactions on Evolutionary Computation(JCR中科院一区,影响因子8.124)上。下面我们对本研究工作的相关成果展开介绍。
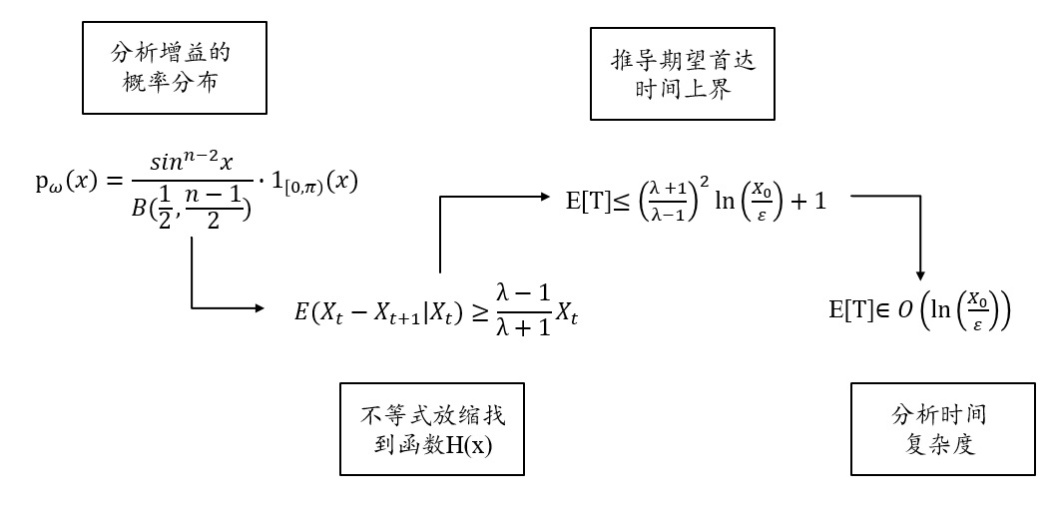
图三 各进化算法分析策略适用范围的韦恩图 首先我们简要介绍采用数学推导方式来分析进化算法的计算时间,其流程如图四所示。该过程先分析每次迭代中解的概率分布,然后推导算法在一次迭代中向全局最优解所靠近的距离的期望(平均增益),计算达到目标精度所需的迭代次数,最终借助渐进性符号来表示计算时间。
图四 数学推导分析进化算法计算时间的流程 其中,平均增益是计算时间分析过程中的重要概念[7]。在进化算法迭代的过程中,增益代表了下一代种群的适应值差与前一代种群的适应值差的差值,其中种群的适应值差 种群最优个体与全局最优解的“距离”。而平均增益则是增益的期望,刻画了进化算法在一次迭代的过程中向最优解靠近的“平均步幅”。 在上述数学推导过程中,前两个步骤实现起来很困难。因为对于第n次迭代,所求解以及增益的概率分布会受到初始解、各种随机化的算子、超参数取值等诸多因素的影响,导致数学推导平均增益需要繁重的分析和计算,有时甚至无法化简分析的结果。
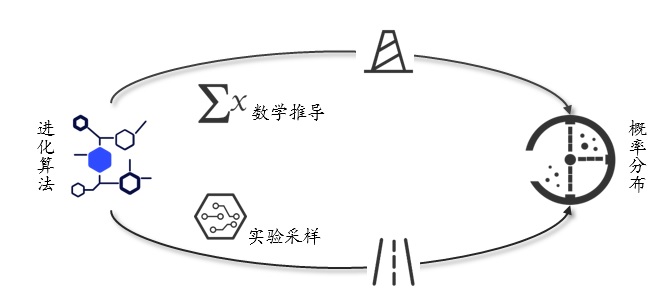
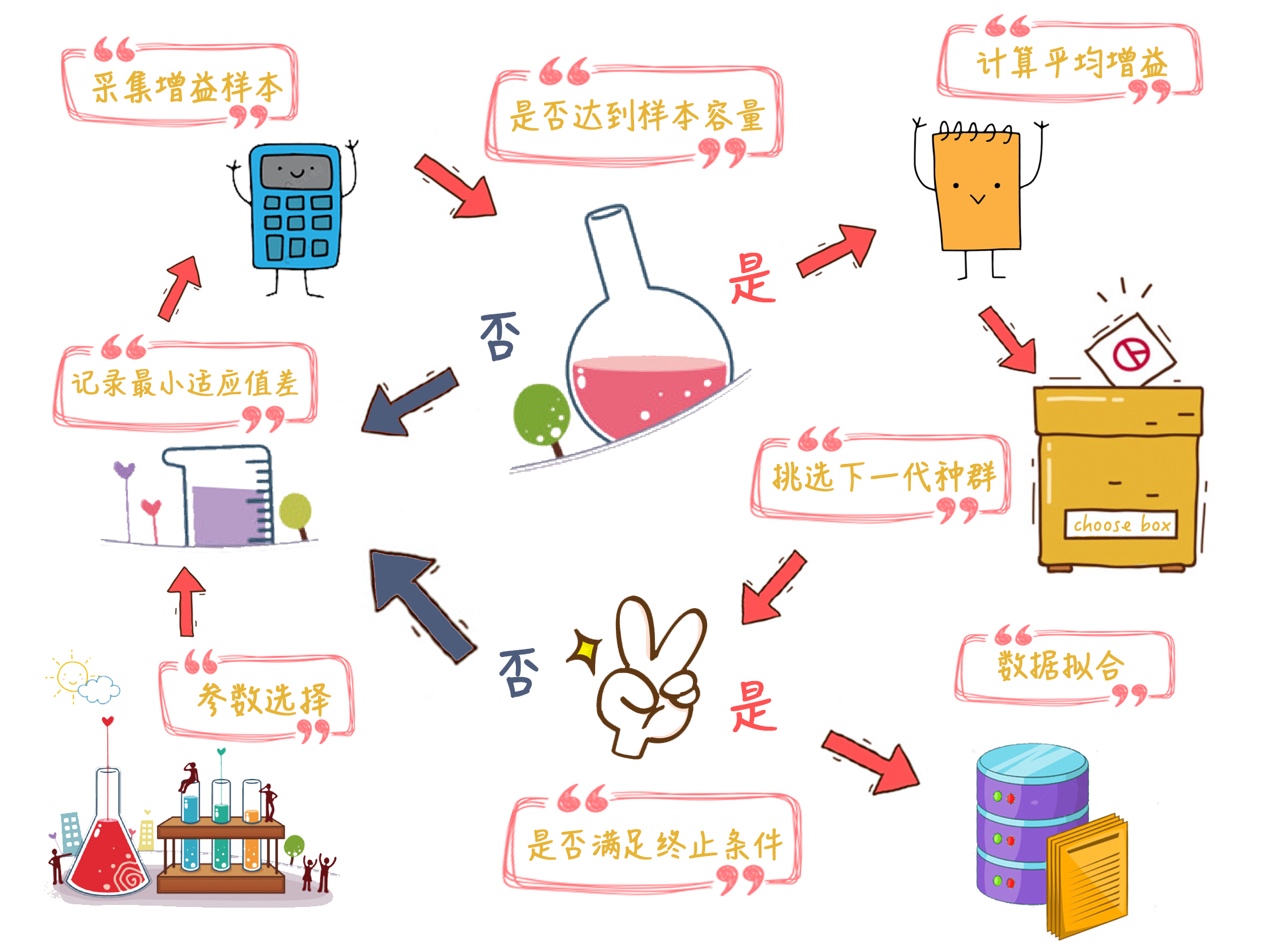
图五 所提估算方法与传统数学推导方法的区别 而本项研究中所提的估算方法则通过实验采样的方式来计算平均增益,从而避开了这个难点,两者的区别如图五所示。该采样实验的思路主要是在一次迭代中,令进化算法产生新解的过程独立地重复若干次,并分别计算新解的增益,从而用增益的平均值来估计增益的期望。上述实验的流程如图六所示,关于该方法的细节请参见引文[1]。
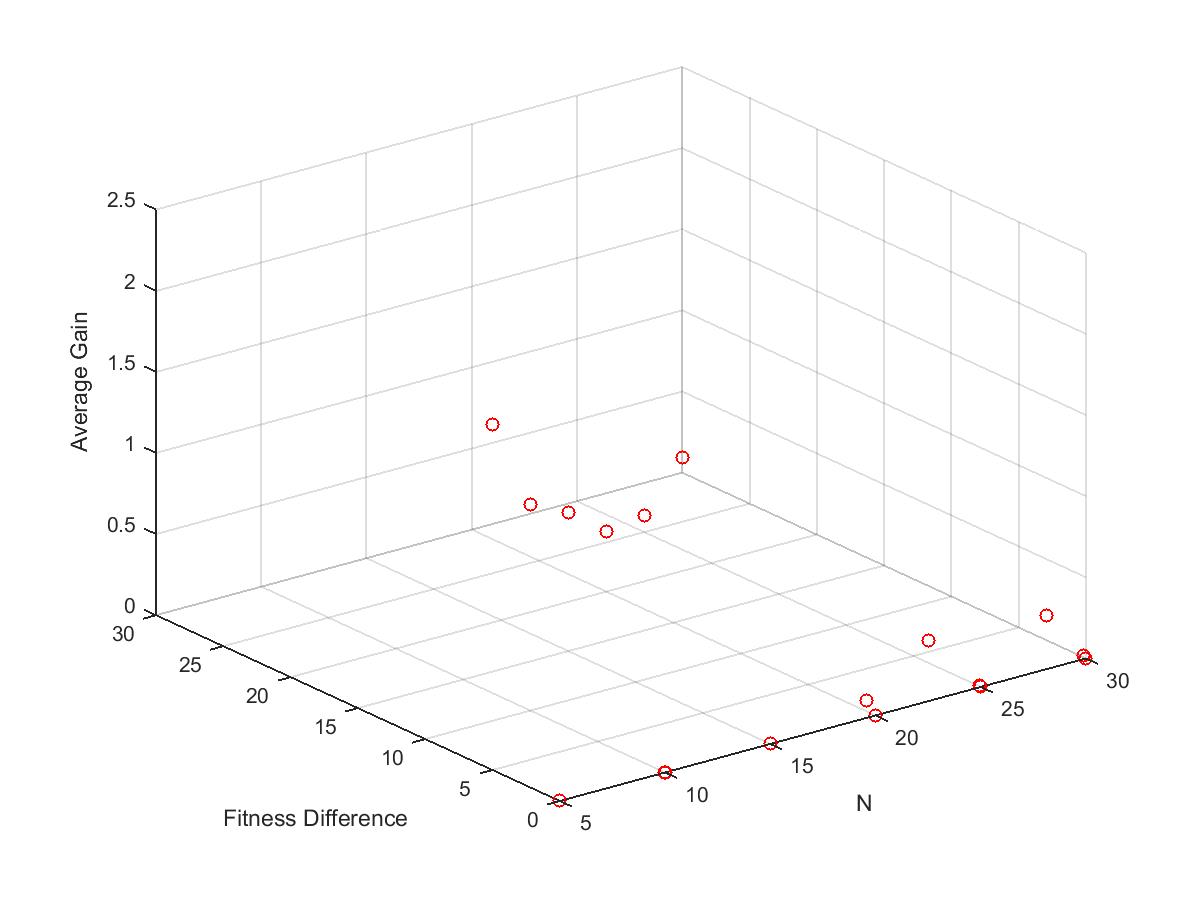
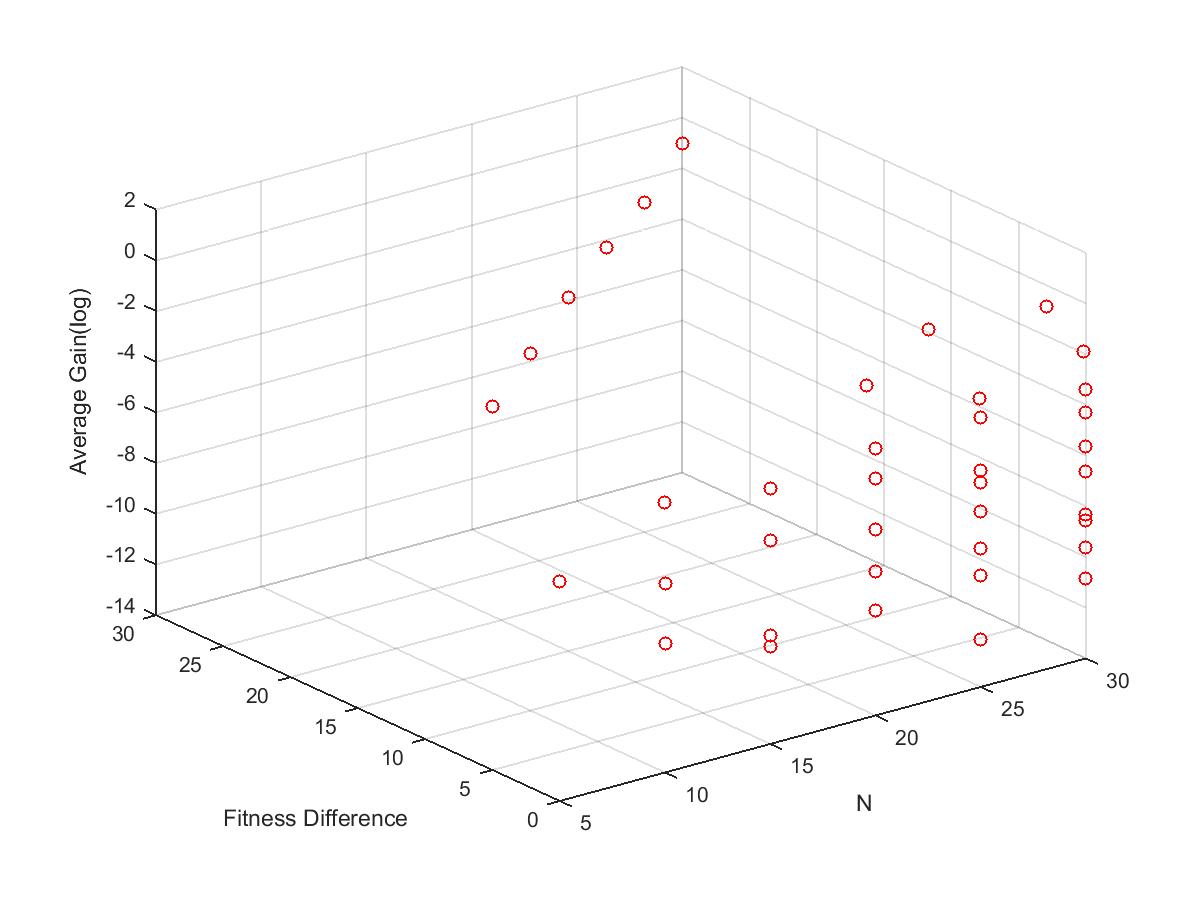
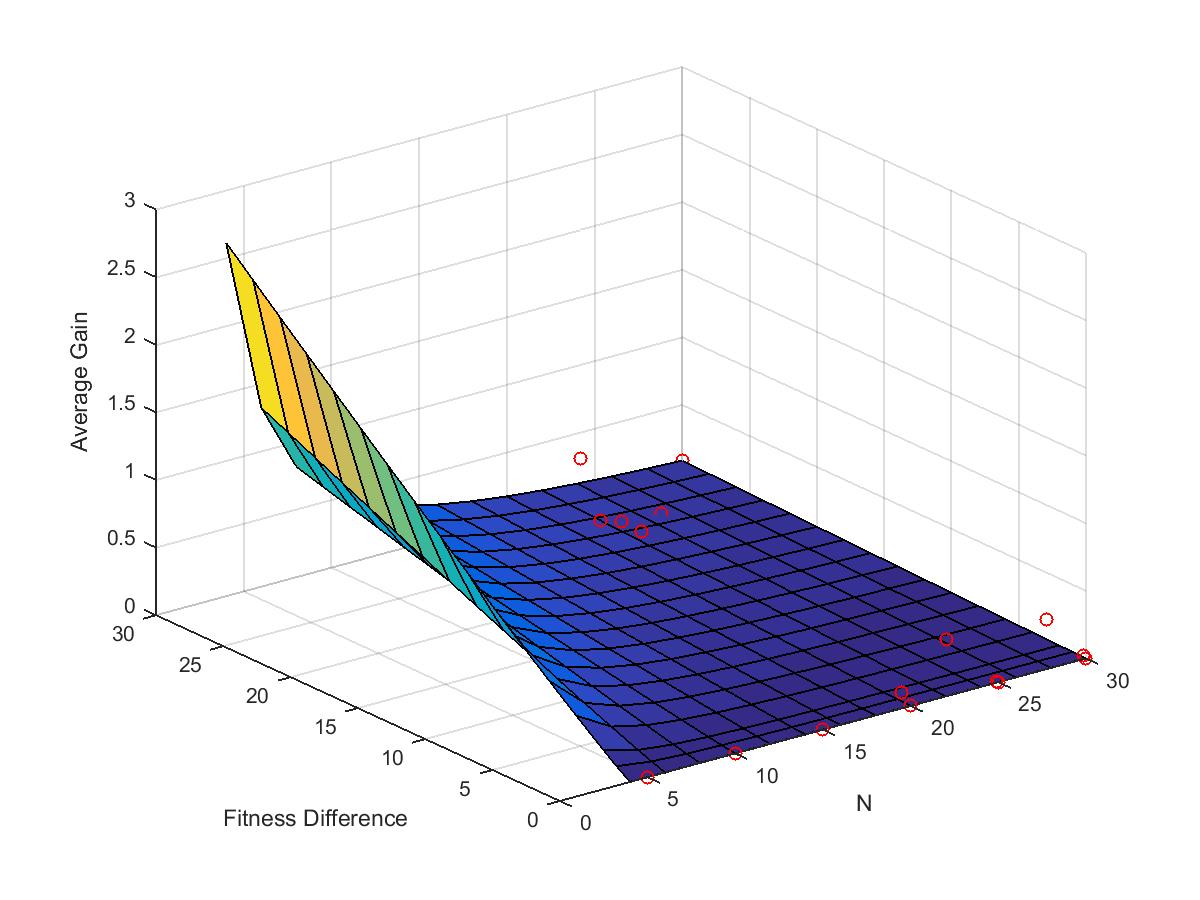
图六 采样实验的流程示意图 根据论文[1]中的定理一表示,如果已知增益的分布,且找到满足特定条件的函数H(x),那么算法的计算时间上界为函数H(x)倒数的积分加一。因此,基于此前收集到的增益样本点,本次实验估算方法采用曲面拟合技术来获得满足条件的函数H(x),从而得到所需求的期望首达时间上界。 下面我们以标准进化策略算法求解球形函数为例,展示该估算方法的使用过程。首先我们遵循上述采样实验的步骤来收集增益的样本,图七展示了所得的平均增益关于问题维度及适应值差图像。接着为了更好地体现数据的特征,我们在图七的基础上对平均增益的数值取以为底的对数,最终得到的效果如图八所示。
图七 平均增益关于问题维度及适应值差图
图八 取对数后平均增益关于问题维度及适应值差图 经过对平均增益数据点的拟合后,我们得到的拟合结果如公式一所示。然后根据平均增益模型定理二,可以推导出期望首达时间的上界,如公式二所示,从而得到所估算进化策略的时间复杂度。其中下面图九,图十分别展示了取对数值前后的样本点及其曲面拟合结果的图像。 公式一 最终得到的拟合结果
公式二 期望首达时间的上界
图九 样本点及其曲面拟合结果图
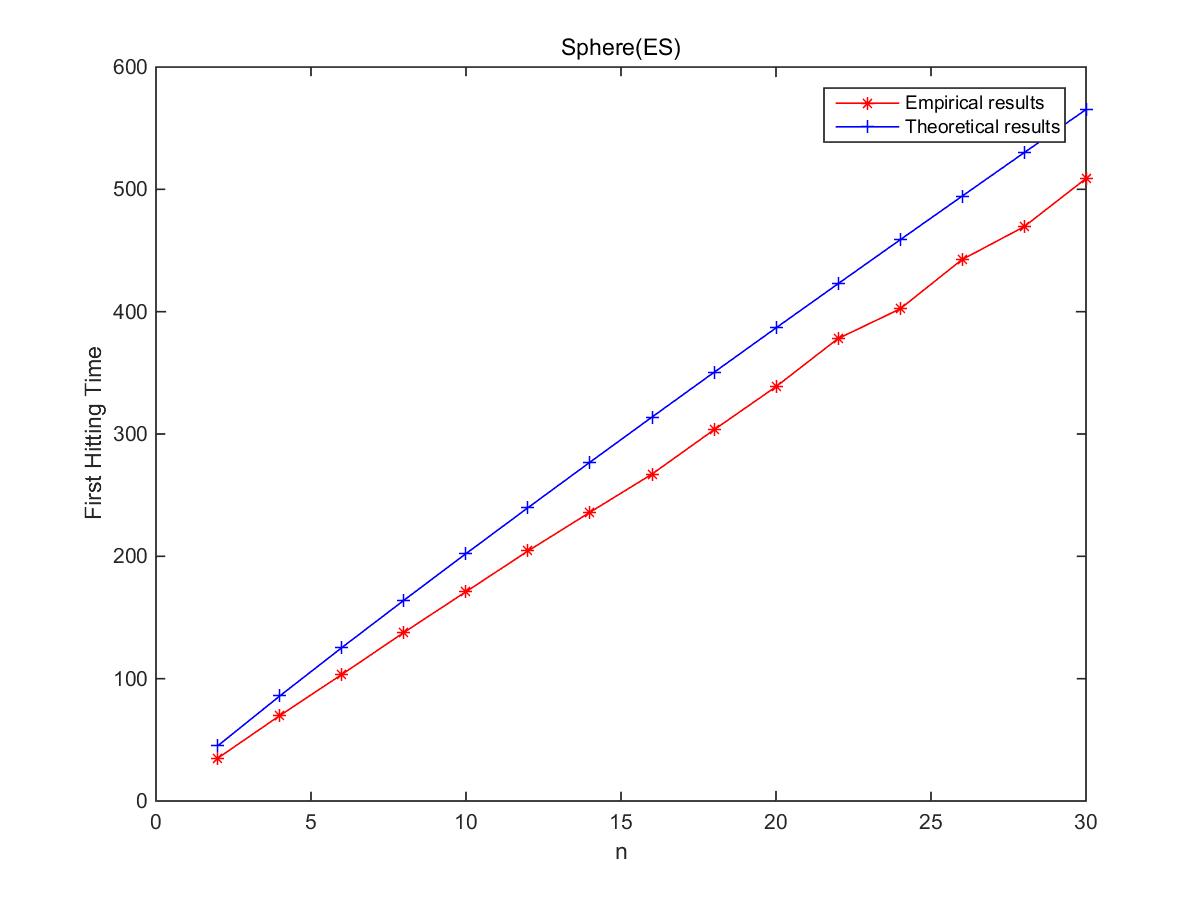
图十 取对数后样本点及其曲面拟合结果图 为了验证所提估算方法的有效性,本次研究还进行了进化策略求解球形函数的数值实验,收集到进化策略求解不同维度的球形函数的计算时间,并与本估算方法得到的计算时间进行对比分析,最终实验结果如下图十一所示。结果表明,估算所得到的上界和实际的平均首达时间相当接近[1],说明该估算方法在分析进化算法的计算时间上具备了极高的准确率。
图十一 实际平均首达时间与估算上界的比较结果 本次研究以平均增益模型作为理论分析框架,使用统计采样实验来辅助估算连续型进化算法计算时间的过程,提出了一种基于平均增益模型的连续型进化算法时间复杂度估算方法。除了平均增益模型外,其他理论分析工具也可以用于讨论各种前沿进化算法的计算时间。近期有一些同行的工作甚至突破了(1+1)EA的结果,不过也是一些理论构造的特例。在未来的工作中,如果把本项工作提出的估算方法引入到层次分析法、漂移分析、转换分析等优秀的分析框架里,将有望得到丰硕的研究成果。
图十二 关于进化算法时间复杂度的讨论 让理论研究助力实际应用是智能算法实验室一直以来的目标,目前智能算法实验室计划搭建自动化的进化算法时间复杂度拟合平台,届时只需提供算法和问题的接口,由平台完成采样实验、曲面拟合、上界推导等工作,即可求得时间复杂度上界。正如上图十二漫画所示,之前使用数学推导来计算进化算法时间复杂度的艰难时代已经过去,现在只要你会编程就可以使用我们的方法来准确高效地分析其计算时间,从而真正打造出一项进化算法的“科学依据”——计算时间复杂度。 参考文献:
校稿:黄翰、冯夫健 图: 苏俊鹏(部分图片来源网络) 实验室负责人: 黄翰教授 联系邮箱: hhan@scut.edu.cn 时间: 2019年10月24日 |