杜晓明
![]()
个人简历:
1999.-2003. 南京大学数学系,数学与应用数学专业,本科
2003.-2009. 北京大学数学科学学院,基础数学专业,博士研究生;导师:姜伯驹院士、王诗宬院士
2009.-2019. 华南理工大学数学系,讲师
2019.-现在 华南理工大学数学学院,副教授
招生方向:基础数学(几何拓扑、几何群论)、应用数学
附1:几何拓扑与几何群论简介
几何拓扑
整个数学,从方法上划分,大致可以分为分析、代数、几何三大块(不过在处理特定的问题时,都是综合运用这三种方法;只要能解决问题,不局限于非要用哪一种方法)。其中几何学主要关心形状,包括大小度量、空间结构等。拓扑学是几何学中的一个重要的分支。
拓扑学是研究一些较深层次不变量的数学方向。譬如:不太考虑物体的大小、距离的远近;而是更关注两块区域是否连通、物体形状能否连续形变、全空间的结构是否相同等等这些更本质的问题。拓扑学主要处理的对象是各种抽象空间,如物理空间、化学分子空间、计算机的抽象概念图空间、代数方程或者微分方程的解空间(从中可以看出拓扑学与其他数学分支如代数几何与泛函分析、乃至拓扑学与其他应用学科或自然学科之间的相互影响)。为了分辨空间的结构与性质,拓扑学创造或者利用了大量的如群、环、纤维丛等工具。
拓扑学从研究工具上划分,大致可分为一般拓扑(或称点集拓扑)、代数拓扑、微分拓扑、几何拓扑(或称低维拓扑)几大类。点集拓扑偏重逻辑的推演;代数拓扑主要借助同伦群、纤维化、示性类等代数的工具刻画空间的结构;微分拓扑在拓扑空间的基础上添加上光滑结构,用微分的手段(如de-Rham同调、微分形式空间的Hodge分解等)反过来处理拓扑的问题;几何拓扑,又称低维拓扑,主要利用几何结构,处理2、3、4维空间中一些更细更精确的结构,如纽结、双曲几何、空间上的动力系统等。虽然拓扑的分支有以上的分类,但在解决实际问题时,也是综合各种方法,很难说以上各个拓扑方向之间有哪些明确的界限。
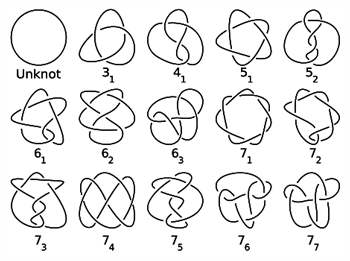
图1:纽结表上前几个较简单的纽结
拓扑学的研究一直处于世界数学发展前沿。数学界的最高奖菲尔兹奖获得者里面,有超过四分之一的工作与拓扑学有关。这些与拓扑学有关的工作里面,年代比较早的多数跟微分拓扑和代数拓扑相关,而年代比较后的多数跟几何拓扑有关。如:
Serre(1954,代数拓扑中的同伦群计算)、
Thom(1958,微分拓扑中的配边理论)、
Milnor(1962,微分拓扑中有多种微分结构的7维怪球)、
Atiyah(1966,微分拓扑中的Atiyah-Singer指标定理)、
Smale(1966,微分拓扑中的广义Poincare猜想)、
Novikov(1970、代数拓扑中的示性类不变量)、
Quillen(1978、代数拓扑中的K理论)、
Thurston(1982,几何拓扑中的叶状结构和3维流形分类)、
Yau(丘成桐)(1982,几何拓扑中的极小曲面问题用分析方法处理)、
Donaldson(1986,微分拓扑中的4维空间怪异微分结构)、
Freedman(1986,几何拓扑中的4维Poincare猜想)、
Jones(1990,几何拓扑中的扭结Jones多项式不变量)、
Witten(1990,几何拓扑与数学物理之间的联系)、
McMullen(1998,几何拓扑中的双曲几何)、
Kontsevich(1998,几何拓扑中的扭结分类)、
Perelman(2006,几何拓扑中的3维Poincare猜想用分析的方法证明)、
Mirzakhani(2014,几何拓扑中的Riemann曲面模空间)。
几何拓扑中的许多问题,都跟其他主要的数学分支发生密切联系。如扭结论在数学物理的量子场论的发展中起作用、低维流形与代数几何发生联系等。反过来几何拓扑的问题也会用其他数学领域中的工具来处理,如Perelman用几何分析解微分方程的手段解决了3维Poincare猜想。
几何群论
几何群论是目前国际上比较新而又非常活跃的研究领域。它研究无限群在带几何结构的对象上的作用,或者甚至把群本身看作几何的对象来研究,建立起群本身的度量空间与被群作用的空间之间的拟等距,反过来研究群本身的结构。几何群论与低维拓扑、双曲几何、Lie群、齐性空间、代数几何、计算群论、微分几何、动力系统、测度论、泛函分析、数理逻辑、概率论、甚至复杂性理论等数学领域都有紧密的联系。
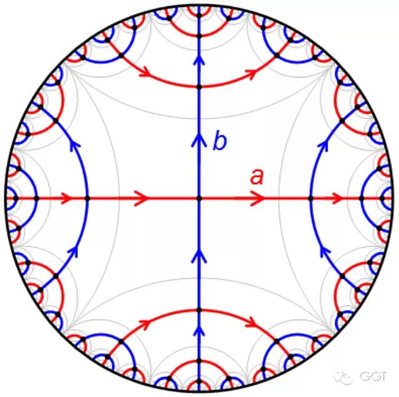
图2:自由群的Cayley图在双曲平面的嵌入

图3:双曲平面中(2,3,7)-Coxeter群的作用轨道
数学界除了菲尔兹奖之外的另一个重要的奖是沃尔夫奖。最近的二三十年里,有不少沃尔夫奖的得奖者在几何群论领域做过十分重要的工作。其中包括:
Gromov(1993年沃尔夫奖,提炼出双曲群的概念,几何群论奠基)、
Tits(1993年沃尔夫奖,Lie群的building结构)、
Margulis(1978年菲尔兹奖,2005年沃尔夫奖,研究Lie群中的格点)、
Sullivan(2010年沃尔夫奖,Klein群与复动力系统的联系)、
Mostow(2013年沃尔夫奖,双曲空间离散等距群的刚性)。
另外,几年之前由阿里巴巴创始人马云、facebook创始人扎克伯格、谷歌创始人布林等人赞助成立的科学突破奖(Breakthrough Prizes)数学奖,在2016年颁给了在低维拓扑与几何群论领域作出惊人贡献的Agol。
目前,因为几何群论与众多数学分支联系的特点,该方向正在国际上蓬勃发展。漂亮的新工具和新方法不断发明产生。这个崭新的领域,正不断吸引着有志向有天赋的年轻数学家。
附2:招生简介
本人招生时遵循有教无类的原则:不论学生以前的背景如何,只要你对我的方向有浓厚的兴趣、并且在研究生阶段愿意下苦功花时间钻研,都十分欢迎你来找我讨论。有志同道合者一起研究数学,是非常快乐的事情。不过需要提醒的是,相对其他数学方向,几何拓扑的论文产出较少,同时又有一定的门槛(需要学过抽象代数里群的概念、需要计算许多无限群的例子),因此几何拓扑方向的研究生毕业也有一定难度。
本人对数学与计算机结合的领域也有浓厚的兴趣,尤其是互联网时代的编程工具结合数学方法的应用。因此也招少量应用数学方向的研究生。
![]()
几何拓扑,曲面映射类群,几何群论
![]()
科研论文:
Du, Xiaoming. On Z2-Thurston norms and pseudo-horizontal surfaces in orientable Seifert 3-manifolds. Topology Appl.312(2022), Paper No. 108060, 17 pp.
Du, Xiaoming. The torsion generating set of the extended mapping class groups in low genus cases. Osaka J. Math.58(2021), no.4, 815–825.
Du, Xiaoming. The torsion generating set of the mapping class groups and the Dehn twist subgroups of non-orientable surfaces of odd genus. Hiroshima Math. J.50(2020), no.2, 199–206.
Xiaoming Du. The Extended Mapping Class Group Can Be Generated by Two Torsions. J. Knot Theory Ramifications, Volume No.26 (2017), Issue No. 11.
Link:http://www.worldscientific.com/doi/abs/10.1142/S0218216517500614
Xiaoming Du. Generating the mapping class groups with torsions. J. Knot Theory Ramifications, Volume 26 (2017), Issue No. 07.
Link:http://www.worldscientific.com/doi/abs/10.1142/S0218216517500377
Xiaoming Du. Non-wandering expanding maps on branched 1-manifolds and Smale-Williams solenoids. Acta Mathematica Sinica (English Series) 30 (2014), no. 6, 1083–1088.
Xiaoming Du. On self-mapping degrees of S^3-geometry manifolds. Acta Mathematica Sinica (English Series) 25 (2009), no. 8, 1243–1252.
科研项目:
国家自然科学基金面上项目 12471075 广义Weyl问题与Teichmuller理论(参与,到账经费8.6万),2025.1.-2028.12.
国家自然科学基金面上项目 11571246 自由群的几何自同构(参与,到账经费5万),2016.1.-2019.12.
国家自然科学基金面上项目 11471248 三维流形上的Anosov流与双曲块(参与,到账经费5万),2015.1.-2018.12.
国家自然科学基金青年基金 11401219 曲面映射类群Dehn twist之间的关系(主持,到账经费22万),2015.1.-2017.12.
中央高校科研业务面上项目 2014ZM0080 曲面映射类群的生成元与关系(主持),2014.1.-2015.12.
![]()
scxmdu(AT)scut(DOT)edu(DOT)cn
4号楼4137

