| 问题1:级数收敛的 必要条件是什么? |
答:
若级数![]() 收敛,那么
收敛,那么![]() .但要注意逆命题不成立,例
.但要注意逆命题不成立,例![]() 发散,但
发散,但![]() 。
。
问题2:怎样判断正项级数的敛散性?
答:
(1)比较判别法。选取敛散性已知的正项级数与所给的级数比较,常用的比较级数有等比级数![]() ,调和级数
,调和级数![]() ,和
,和![]() 级数
级数![]() 。
。
例:判断![]() 的敛散性。当
的敛散性。当![]() 时,
时,![]() ,又
,又![]() 发散,所以
发散,所以![]() 发散。
发散。
或用极限形式比较判别法:因为![]() 发散,又
发散,又![]() ,所以
,所以![]() 发散。
发散。
(2)比值判别法或根值判别法。例:判断![]() 的敛散性。因为
的敛散性。因为![]()
![]() ,所以
,所以![]() 收敛。
收敛。
问题3:怎样判断任意项级数的发散性?
答:
(1)对于任意项级数,首先考察通项是否趋向于零,若不趋向于零,则级数发散。例:![]() ,因为
,因为![]() ,所以
,所以![]() 发散。
发散。
(2)如果是用比值法或根值法判断知其绝对值级数发散,则原级数也发散。
例: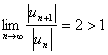 ,知
,知问题4:下列命题是否正确?
(1)若![]() 收敛,且
收敛,且![]() ,则
,则![]() 收敛。
收敛。
答:
(1)当![]() ,
,![]() 时,命题正确,否则不一定正确。例
时,命题正确,否则不一定正确。例![]() ,
,![]() 。
。
答:
由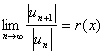 ,令
,令![]() ,得级数的收敛区间,再考察级数在收敛区间端点的收敛性。例:
,得级数的收敛区间,再考察级数在收敛区间端点的收敛性。例:![]() ,
,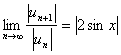 ,令
,令![]() ,得
,得![]() 。当
。当![]() 时,
时,![]() ,级数为
,级数为![]() 或
或![]() 均收敛,所以收敛域为
均收敛,所以收敛域为![]() 。
。
答:
应用幂级数的性质:幂级数在其收敛区间内可以逐项求导和逐项积分,将已知级数化为等比级数或几个常见的级数求和,在施以逆运算求得所给级数的和函数。
例:![]()
![]() 。设和函数为
。设和函数为
问题7:怎样求幂级数的和函数?
答:
应用幂级。因为![]() ,即
,即![]() 。
。
记![]()
![]() ,有
,有![]() ,则
,则![]() ,于是
,于是
答:
一般应用间接法将函数在![]() 点展开成Taylor级数。要熟悉几个常用函数(
点展开成Taylor级数。要熟悉几个常用函数(![]() )的Maclaurin展开式,结合对级数进行逐项求导或逐项积分的运算。其中:
)的Maclaurin展开式,结合对级数进行逐项求导或逐项积分的运算。其中:
![]() ,
,
![]() ,
,
![]() ,
,
![]() 。
。
例(1)![]() .
.
将![]() 化为
化为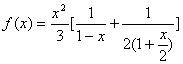 ,
,
所以![]() 。
。
例(2)![]()
将![]() 化为
化为![]() ,
,
问题9:将函数在![]() 点展开成Fourier级数必须掌握什么?
点展开成Fourier级数必须掌握什么?
答:
(1)会求Fourier系数,
(2)会作延拓(奇、偶延拓,周期延拓),
(3)知道Dirichle定理,并依此画出和函数的图形。