| 问题1:第二型曲线积分共有哪几种计算方法? |
答:
方法一:化第二型曲线积分为定积分。
方法二:利用格林公式化第二型曲线积分为二重积分
方法三:利用斯托克斯公式化第二型曲线积分为第二型曲面积分
方法四:利用第二型曲线积分与路径无关的条件,如果曲线积分与路径无关,选取特殊路径计算第二型曲线积分
例1:求![]() ,其中
,其中![]() 是从点
是从点![]() 到
到![]() 再到
再到![]() 的折线。
的折线。
解:线段![]() 的参数方程为:
的参数方程为:![]() ,
,![]() 从0变到1;线段
从0变到1;线段![]() 的参数方程为:
的参数方程为:![]() ,
,![]() 从0变到1。
从0变到1。
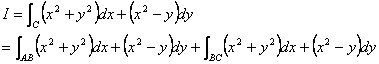
![]()
![]()
例2:![]()
![]() 为椭圆
为椭圆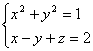 且从
且从![]() 轴正方向看去,
轴正方向看去,![]() 顺时针。
顺时针。
解:曲线![]() 的参数方程为:
的参数方程为:![]() ,
,![]() 从
从![]() 变到0。
变到0。
![]()
![]() 。
。
注:在计算第二类曲线积分题时,其中最关键的是找到积分路径的恰当的参数方程,确定起点和终点对应的参数值。当积分路径不能用同一个参数方程表示时,则可把积分路径分解成若干段来处理,如例1。第二类曲线积分转化成定积分时,下限为起点对应的参数值,上限为终点对应的参数值,所以上限有时可能比下限小,如例2。
例3:计算曲线积分![]() ,其中
,其中![]() 是园
是园![]() 并取逆时针方向。
并取逆时针方向。
解:设![]()
![]()
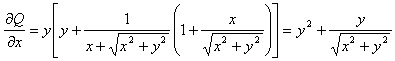
![]()
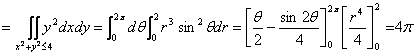
注:在利用格林公式计算第二型曲线积分时,特别要注意积分路径的方向及![]() 在所考虑闭区域的连续可导性。积分路径还要是封闭曲线;如果不是,要添加辅助线构成封闭曲线后才能用公式。
在所考虑闭区域的连续可导性。积分路径还要是封闭曲线;如果不是,要添加辅助线构成封闭曲线后才能用公式。
例4:利用斯托克斯公式计算![]() ,其中
,其中![]() 是平面
是平面![]() 与柱面
与柱面![]() 的交线,若从
的交线,若从![]() 轴正向看去,
轴正向看去,![]() 取逆时针。
取逆时针。
解:曲线![]() 围成的曲面
围成的曲面![]() 为
为![]() ,利用右手准则应取上侧,
,利用右手准则应取上侧,
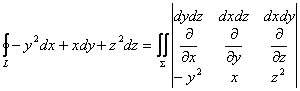
![]()
![]()
注意这里![]() 。
。
注:曲面![]() 的选取是不唯一的,只要
的选取是不唯一的,只要![]() 是以
是以![]() 为边,
为边,![]() 前面的函数在
前面的函数在![]() 上具有连续的偏导数就可以,但选取不同的
上具有连续的偏导数就可以,但选取不同的![]() 化成的第二型曲线积分的计算难易程度不一样。所以在用此种方法计算第二型曲线积分时,值得多花点时间选取一个恰当的
化成的第二型曲线积分的计算难易程度不一样。所以在用此种方法计算第二型曲线积分时,值得多花点时间选取一个恰当的![]() 以降低计算难度及计算量。
以降低计算难度及计算量。
例5:计算曲线积分![]() ,其中
,其中![]() 为沿摆线
为沿摆线![]() 从点
从点![]() 到点
到点![]() 的弧。
的弧。
解:设![]()
因为![]() ,所以此曲线积分与路径无关,选取积分曲线为从
,所以此曲线积分与路径无关,选取积分曲线为从![]() ,经过点
,经过点![]() 到点
到点![]() 的折线
的折线![]() ,则有
,则有
![]()
![]()
![]() +
+![]()
![]()
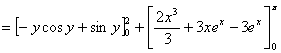
![]()
问题2:如果P,Q在简单闭曲线C所围成的区域内有偏导数不存在的点,第二型曲线积分![]() 能否运用格林公式计算?如果能还应注意什么问题?
能否运用格林公式计算?如果能还应注意什么问题?
答: 当闭曲线所围成的区域是多连通的时,格林公式还是成立。因此,如果函数P,Q在所考虑的闭区域内只有有限个偏导数不存在的点时,可以把他们挖去。然后对多连通区域运用格林公式。在挖去这些偏导数不存在的点时,挖出的洞的形状是不唯一的,虽然,他们对计算结果没有影响,但是会影响计算的难易程度。因此,针对具体的题目,我们应选取一个恰当的形状来挖掉这些点,以减少计算量。我们来看下面的例子来说明这一点。
例1:计算积分![]() ,其中
,其中![]() 为
为![]() 的正方向。
的正方向。
解:![]()
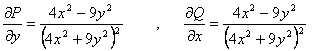
当![]() 时有
时有![]()
1)当![]() 时,利用格林公式有
时,利用格林公式有
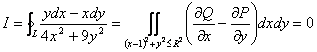
2)当![]() 时,
时,![]() 在
在![]() 的内部,如右图
的内部,如右图
方法一、取充分小的正数![]() ,用在
,用在![]() 的椭圆
的椭圆
![]() 把
把![]() 点挖掉
点挖掉
利用格林公式有
![]()
![]()
所以![]() ,又因为
,又因为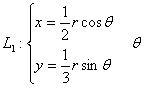 从
从![]() 变到
变到![]()
![]()
方法二、取充分小的正数![]() ,用在
,用在![]() 的圆
的圆
![]() 把
把![]() 点挖掉
点挖掉
利用格林公式有
![]()
![]()
所以![]() ,又因为
,又因为![]() 从
从![]() 变到
变到![]()
![]()
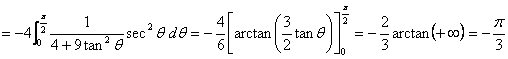
方法三、取充分小的正数![]() ,用在
,用在![]() 的正方形
的正方形
![]()
把![]() 点挖掉。利用格林公式有
点挖掉。利用格林公式有
![]()
![]()
所以![]() ,又因为
,又因为![]() 从
从![]() 变到
变到![]()
![]() 从
从![]() 变到
变到![]() ;
;![]() 从
从![]() 变到
变到![]() ;
;
![]() 从
从![]() 变到
变到![]()
![]()
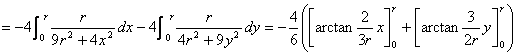
![]()
![]()
问题3:第二型曲面积与第一型曲面积分有什么联系?什么情况下第二型区面积分化为第一型曲面积分计算较简洁?
![]()
![]()
其中![]() 是与积分曲面
是与积分曲面![]() 所取侧相对应的单位法向量。
所取侧相对应的单位法向量。
答: 不论是第一型曲面积分还是第二型曲面积分,其基本计算方法都是利用投影法把曲面积分化为二重积分。但是第一型曲面积可以较自由地选取投影坐标面,而第二型曲面积分则不能。因此在用投影法计算第二型曲面积分时,当积分曲面投影到对应坐标面上的区域很难确定或不能确定时,就可考虑把第二型曲线积分化为第一型曲线积分后再计算。
我们来看下面的例子。
例1:计算![]() ,其中
,其中![]() 是锥面
是锥面![]() 被平面
被平面![]() 所截下的有限部分下侧。
所截下的有限部分下侧。
注:此题如果运用第二类曲面积分的基本方法计算非常繁杂,因为,用基本方法做要考虑曲面对三个坐标面的投影,计算量很大,若把它转化为第一类曲面积分,就只须向一个坐标面投影,可大大简化计算。
解:我们考虑把以上曲面积分化为第一类曲面积分,此曲面上一点处的法向量为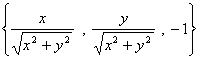 因为是取下侧,所以
因为是取下侧,所以![]() 轴的坐标应为负值。此法向量的单位向量为
轴的坐标应为负值。此法向量的单位向量为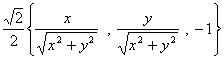 。且此曲面在
。且此曲面在![]() 面上的投影为圆盘
面上的投影为圆盘![]()
![]()
![]()
![]()
问题4:在第二型曲面积分化为第一型曲面积分时,怎样确定单位法向量![]() ?
?
答: 在第二型曲面积分转化为第一类曲面积分时,关键是怎样确定指向定向曲面![]() 所指定的一侧的法向量,基本方法如下:
所指定的一侧的法向量,基本方法如下:
1)如果指的是上侧,法向量![]() 轴坐标为正,指的是下侧,法向量
轴坐标为正,指的是下侧,法向量![]() 轴坐标为负;
轴坐标为负;
2)如果指的是右侧,法向量![]() 轴坐标为正,指的是左侧,法向量
轴坐标为正,指的是左侧,法向量![]() 轴坐标为负;
轴坐标为负;
3)如果指的是前侧,法向量![]() 轴坐标为正,指的是后侧,法向量
轴坐标为正,指的是后侧,法向量![]() 轴坐标为负;
轴坐标为负;
例如曲面![]() 的解析式为
的解析式为![]() ,其法向量为
,其法向量为![]() 。
。
如果指的是上侧(此时![]() ),对应的法向量为
),对应的法向量为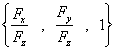 ,如果指的是下侧
,如果指的是下侧
(此时![]() ),对应的法向量为
),对应的法向量为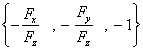 ;
;
如果指的是右侧(此时![]() ),对应的法向量为
),对应的法向量为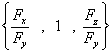 ,如果指的是左侧
,如果指的是左侧
(此时![]() ),对应的法向量为
),对应的法向量为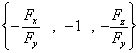 ;
;
如果指的是前侧(此时![]() ),对应的法向量为
),对应的法向量为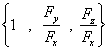 ,如果指的是后侧
,如果指的是后侧
(此时![]() ),对应的法向量为
),对应的法向量为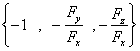 。
。
最后再把他们化为单位向量。
例1:已知![]() 是平面
是平面![]() 在第一象限的部分并取下侧,求其对应的单位法
在第一象限的部分并取下侧,求其对应的单位法
向量。
解:其对应法向量为![]() ,其中因为是取下侧
,其中因为是取下侧![]() 轴坐标为负。其对应的单位
轴坐标为负。其对应的单位
法向量为![]() 。
。
例2:已知![]() 是柱面
是柱面![]() 介于平面
介于平面![]() 之间的部分的外侧,求其对应
之间的部分的外侧,求其对应
的单位法向量。
解:此曲面必须分成两块来处理,一块的解析式为![]() 并取右侧;一块的解
并取右侧;一块的解
析式为![]() 并取左侧。他们分别对应的单位法向量为
并取左侧。他们分别对应的单位法向量为
![]()
![]()
答: 被积函数![]() 的值是取于曲线
的值是取于曲线![]() 上。
上。![]()
![]()
![]() ,所以,曲线积分的值,取决于被积函数与给定的曲线。
,所以,曲线积分的值,取决于被积函数与给定的曲线。
答: 第一型曲线积分中![]() 是弧长,因此在计算中要保证其非负性,这体现在将其化成定积分,在确定积分限时,应使上限不小于下限;
是弧长,因此在计算中要保证其非负性,这体现在将其化成定积分,在确定积分限时,应使上限不小于下限;
问题7:如何看待向量函数的曲线积分?
答: 通常第二型曲线积分以组合积分形式出现:
![]() ,
,
这也可以视为向量函数![]() 的曲线积分,表示成简洁的向量点积形式:
的曲线积分,表示成简洁的向量点积形式:
![]()
答: 定义完全类似于平面第二型曲线积分,设有向量函数
![]()
及空间曲线![]() 对应的弧微分向量
对应的弧微分向量![]()
则![]()
问题9:何谓二元函数![]() 在平面曲线
在平面曲线![]() 上连续?
上连续?
答: ![]() 也表示曲线
也表示曲线![]() 上的点集,点
上的点集,点![]()
![]()
![]() 。
。
定义如果![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() ,有
,有![]() 则称二元函数
则称二元函数![]() 在曲线
在曲线![]() 上点
上点![]() 连续。
连续。
函数![]() 在曲线
在曲线![]() 上点
上点![]() 连续的另一种形式是:
连续的另一种形式是:
![]() ,
,![]()
![]()
![]()
![]() .
.
![]() ,
,![]() 在复连通区域D
在复连通区域D![]()
![]() 内连续,且
内连续,且
![]() 但是,
但是,![]() ,其中C是包含原点的一条光滑封闭曲线。
,其中C是包含原点的一条光滑封闭曲线。
事实上,取C是单位圆:![]() ,
,![]() ,
,![]() ,有
,有
![]()
![]()
![]()
![]()
![]()
答: 格林公式是平面曲线积分中的一个重要公式,它将闭路径的曲线积分与相应的一个二重积分联系起来。格林公式的实质是将二元函数偏导数在![]() 上的二重积分化成在
上的二重积分化成在![]() 的边界上的曲线积分,即
的边界上的曲线积分,即![]() 。
。
答: 1)公式使用的条件是![]() 的偏导数在
的偏导数在![]() 中连续,不满足该条件的不能使用此公式。
中连续,不满足该条件的不能使用此公式。
2)看一下书上的证明过程,可以看到
![]()
这实质上就是一元函数的牛顿-莱布尼兹公式,因为这里的![]() 是固定的“常数”。
是固定的“常数”。
3)为了便于记忆格林公式,并与以后的Stokes公式统一,可将其用行列式形式表示成
![]()
答: 有。曲线积分的中值定理是:
若函数![]() 在有界闭的曲线段
在有界闭的曲线段![]() (二点A与B也属于C)上连续,则在曲线
(二点A与B也属于C)上连续,则在曲线![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 其中
其中![]() 表示曲线
表示曲线![]() 的长。
的长。