| 问题1:什么是X型区域?什么是Y型区域? |
答:
在平面区域中,有两类特殊的区域是最具代表性的。
X型区域指区域用集合可表示为:
![]()
其特点是![]() ,则直线
,则直线![]() 至多与区域
至多与区域![]() 的边界交于两点;
的边界交于两点;
Y型区域指区域用集合可表示为:
![]()
其特点是![]() ,则直线
,则直线![]() 至多与区域
至多与区域![]() 的边界交于两点。
的边界交于两点。
问题2:如何计算X型区域和Y型区域上的二重积分呢?
答:
方法是化二重积分为二次积分(累次积分):
![]() ,
,![]() ;
;
问题3:如何选择积分次序呢?
答:
例1:求![]() ,?其中
,?其中![]() 是一以
是一以![]() 为顶点的三角形区域。
为顶点的三角形区域。
解:因为![]() 不能用初等函数表示,所以必须先关于变量
不能用初等函数表示,所以必须先关于变量![]() 积分:
积分:
![]()
![]()
![]()
![]() 。
。
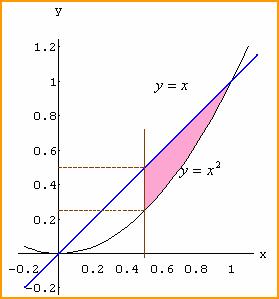
例2:求![]()
![]() 。
。
解:因为![]() 不能用初等函数表示,所以必须先改变积分次序:
不能用初等函数表示,所以必须先改变积分次序:
![]()
![]()
![]() 。
。
例3:求![]() ,其中
,其中![]() 是由
是由![]() 所围的闭区域。
所围的闭区域。
解:因为关于![]() 的积分计算较麻烦,所以先关于
的积分计算较麻烦,所以先关于![]() 积分:
积分:
![]()
![]()
![]()
问题4:怎样在极坐标系下计算二重积分?
答:
I=![]() =
=![]()
![]()
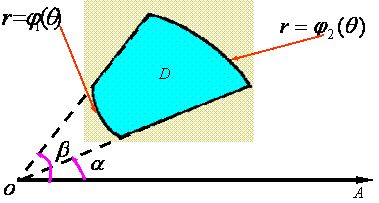
I![]() 。
。
例;写出积分![]() 的极坐标二次积分形式,积分区域为;
的极坐标二次积分形式,积分区域为;
![]() 。
。
答:
当积分区域是圆域或是圆域的部分或被积函数的形式为![]() 时,采用极坐标来计算往往简便得多。
时,采用极坐标来计算往往简便得多。
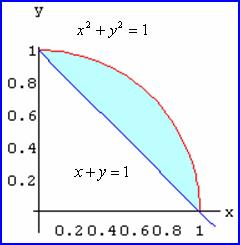
值得注意的是,有时需要同时考虑积分区域和被积函数,例如![]() ,
,![]() 。积分区域为扇形,若单从积分区域考虑,应该选用极坐标系,但计算很繁;此题选用直角坐标系来计算很简单。这时
。积分区域为扇形,若单从积分区域考虑,应该选用极坐标系,但计算很繁;此题选用直角坐标系来计算很简单。这时
![]() =
=![]()
答:
当积分区域与被积函数都有某种对称性,像定积分一样,正确应用对称性将简化积分。
(1)若![]() 关于
关于![]() 轴对称,记
轴对称,记![]() 轴上方部分区域为
轴上方部分区域为![]() ,则
,则
若![]() 关于
关于![]() 为奇函数,那么
为奇函数,那么![]() ;
;
若![]() 关于
关于![]() 为偶函数,那么
为偶函数,那么![]() 。
。
(2)若![]() 关于
关于![]() 轴对称,记
轴对称,记![]() 轴右方部分区域为
轴右方部分区域为![]() ,则
,则
若![]() 关于
关于![]() 为奇函数,那么
为奇函数,那么![]() ;
;
问题7:怎样化定积分为二重积分?
答:
![]() ,其中
,其中![]() 。
。
答:
(1)将三重积分化为一个定积分接一个二重积分(投影法):
设![]() 是一个双曲顶柱体,其底面方程是
是一个双曲顶柱体,其底面方程是![]() ,顶面方程是
,顶面方程是![]() ,它在
,它在![]() 平面的投影区域为
平面的投影区域为![]() ,
,
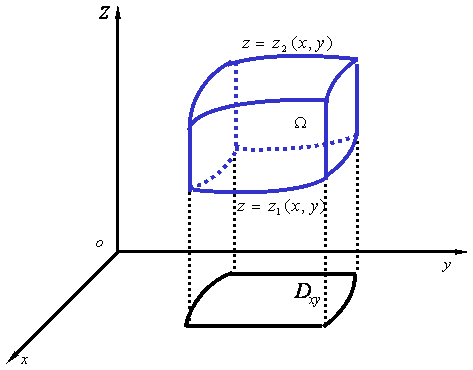
即![]() ,则
,则
![]() 。
。
例 计算三重积分![]() ,其中
,其中![]() 为三个坐标面及平面
为三个坐标面及平面![]() 所围成的闭区域。
所围成的闭区域。
解:![]() 如图
如图

![]()
![]()
![]()
![]()
![]() 。
。
(2)将三重积分化为一个二重积分接一个定积分(截面法):
把积分区域![]() 向某轴(例如
向某轴(例如![]() 轴)投影,得投影区间
轴)投影,得投影区间![]() ;
;
对![]() 用过
用过![]() 轴且平行
轴且平行![]() 平面的平面去截
平面的平面去截![]() ,得截面
,得截面![]() ,
,
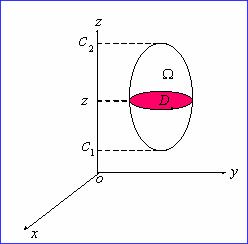
则,![]() 。
。
例 计算三重积分![]() ,其中
,其中![]() 是由椭球面
是由椭球面![]() 所成的空间闭区域。
所成的空间闭区域。
解:![]() 如图
如图

原式![]() ?,因为
?,因为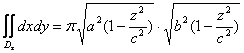
![]() 所以,原式
所以,原式![]()
![]() 。
。
问题9:在柱面坐标系下怎样计算三重积分?
答:柱面坐标系下三重积分计算法本质上就是直角坐标系下的投影法,当完成定积分后,将余下的二重积分化为极坐标系下的二重积分。
当积分区域由球面(或是球面的部分)和圆锥面所围,或被积函数的形式为![]() 时,采用球面坐标来计算往往简便得多。
时,采用球面坐标来计算往往简便得多。
例4 求曲面![]() 与
与![]() 所围成的立体体积。
所围成的立体体积。
解:
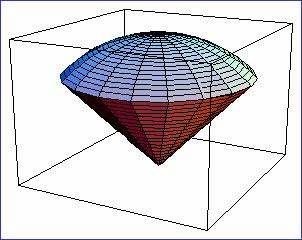
由三重积分的性质知 ![]()
答:
曲线积分的被积函数定义在曲线上,各变量不是独立的,它们受曲线的方程约束,故实际上是一元函数。
曲面积分的被积函数定义在曲面上,各变量不是独立的,它们受曲面的方程约束,故实际上是二元函数。