| 问题1:多元函数的极限与一元函数极限的定义有何不同? |
答: 多元函数的比一元复杂,定义上看起来类似,但有本质的区别。一元函数在一维直线上定义,或左或右趋近方式只有两个方向,多元函数要点![]() 以“任意方式”趋向于点
以“任意方式”趋向于点![]() 。这里的“任意方式”不仅包括任意方向,还包括任何路径。
。这里的“任意方式”不仅包括任意方向,还包括任何路径。
问题2:![]() 使得在函数
使得在函数![]() 的定义域内满足
的定义域内满足![]() ,
,![]() 的一切均有
的一切均有![]() 成立,则
成立,则![]() ,对吗?
,对吗?
答: 不对,原因是这里不只是去心,而且去了两条直线![]() 和
和![]() 上的点。如果改为:
上的点。如果改为:![]() 使得在函数
使得在函数![]() 的定义域内满足
的定义域内满足![]() ,
,![]() ,且
,且![]() 的一切均有
的一切均有![]() 成立,则
成立,则![]() 。那么就等价了。
。那么就等价了。
问题3:关于二重极限的定义有下列两种典型的不同说法,试分析比较它们之间的差异何在?
定义1 设函数 z=f(x,y)在点![]() 的某一邻域内有定义(点 P0可以除外)。如果对于每一个任意给定的正数ε,总存在一个正数δ,使得对于适合不等式
的某一邻域内有定义(点 P0可以除外)。如果对于每一个任意给定的正数ε,总存在一个正数δ,使得对于适合不等式
![]() 的一切点 P(x,y),所对应的函数值 f(x,y) 都满足不等式
的一切点 P(x,y),所对应的函数值 f(x,y) 都满足不等式![]() 。
。
那末,常数A就称为函数![]() 当
当![]() ,
,![]() 时的极限。
时的极限。
定义2 设函数 z=f(x,y) 在点 P0的任一邻域中,有不属于函数定义域D的点,但又总有异于 P0 的属于D的点(即点 P0是D的聚点)。如果对于任意给定的正数ε,总存在一个正数δ,使得对D内适合不等式
![]() 的一切点 P(x,y),所对应的函数值f(x,y)都满足不等式
的一切点 P(x,y),所对应的函数值f(x,y)都满足不等式![]() 。那末,常数A就称为函数
。那末,常数A就称为函数![]() 当
当![]() ,
,![]() 时的极限。
时的极限。
答:
这两种定义的差异主要在于对函数的前提假设不尽相同。前者要求![]() 在点
在点![]() 的某一个去心邻域内都有定义,而后者允许
的某一个去心邻域内都有定义,而后者允许![]() 在点
在点![]() 的任一去心邻域内都有使
的任一去心邻域内都有使![]() 无定义的点。相应地,定义1要求
无定义的点。相应地,定义1要求![]() 的去心邻域内的P都适合
的去心邻域内的P都适合![]() ,而定义2只要求上述邻域内使
,而定义2只要求上述邻域内使![]() 有定义的点P适合
有定义的点P适合![]() 。可见,定义1对函数的要求高,因而使一些极限无法讨论,限制了极限的应用。而定义2放宽了对函数的要求,从而使极限概念更便于应用。
。可见,定义1对函数的要求高,因而使一些极限无法讨论,限制了极限的应用。而定义2放宽了对函数的要求,从而使极限概念更便于应用。
这种概念上的差异,也导致计算上的差异。
例1、计算二重极限![]()
解:依定义1,此极限无意义,因在点(0,0)的任意![]() 邻域内,总存在点
邻域内,总存在点![]() 、
、![]() 、
、![]() 、
、![]() ,使
,使![]() 无定义,当然在这些点不等式
无定义,当然在这些点不等式![]() 就没有意义。
就没有意义。
但根据定义2(允许不考虑Ox轴、Oy轴上的点)有
![]() 。
。
这是因为![]() ,而当
,而当![]() 时,
时,![]() 。
。
例2、计算极限![]()
解:依定义1,此极限无意义,依定义2可以不考虑Oy轴上![]() 的点。通常可见到如下解法:
的点。通常可见到如下解法:
![]() 。
。
(*)处的等号两边的两个极限并不等同,左端极限允许不考虑Oy轴上![]() 的点,但却未允许不考虑Ox轴上
的点,但却未允许不考虑Ox轴上![]() 的点;而右端极限却允许不考虑Ox轴上的点,因此等式右边等于0不能导出等式左边也等于0。
的点;而右端极限却允许不考虑Ox轴上的点,因此等式右边等于0不能导出等式左边也等于0。
正确的解法是:对一切![]() 的点
的点
![]() 。
。
任给![]() ,存在
,存在![]() ,则当
,则当![]() ,且
,且![]() 时,必有
时,必有
![]()
问题4:如果![]() ,其中
,其中![]() 为与θ无关的常数,是否必有
为与θ无关的常数,是否必有![]() ?
?
不是,而且通常情况下没有这个结论。例如极限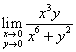 不存在只要用
不存在只要用![]() 验证即得。但若用代换:
验证即得。但若用代换:![]() ,则有
,则有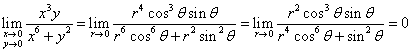 ,这里错在第一个等号没有考虑到
,这里错在第一个等号没有考虑到![]() 时
时![]() 时的情况。
时的情况。
答: 不能。例如函数
![]() 。
。
当动点![]() 沿着y轴
沿着y轴![]() 无限趋近于点(0,0)时,有
无限趋近于点(0,0)时,有
![]() 。
。
且当动点![]() 沿着任意一条直线
沿着任意一条直线![]() (k为任意实数)无限趋近于点(0,0)时,都有
(k为任意实数)无限趋近于点(0,0)时,都有
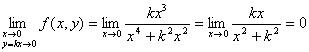 。
。
但是,当动点![]() 沿抛物线
沿抛物线![]() 无限趋近于点(0,0)时,有
无限趋近于点(0,0)时,有
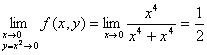 。
。
所以,函数![]() 当
当![]() 时,极限不存在。
时,极限不存在。
答:不一样。前一极限为二重极限,两个自变量是独立的没有先后次序的变化的。后一极限是累次极限的二次极限,它本质上属于一元函数极限的范畴。需要指出的是:如果二重极限和累次极限都存在,那么它们一定相等的。
问题7:判定二重极限不存在,有哪些常用方法?
答:
依二重极限的定义,![]() 存在,要求点
存在,要求点![]() 以任何方式趋向于点
以任何方式趋向于点![]() 时,
时,![]() 有相同的极限。因此判定二重极限不存在,常用方法有如下两种:
有相同的极限。因此判定二重极限不存在,常用方法有如下两种:
1、选取一种![]() 的方式,记为
的方式,记为![]() ,其中C为在函数定义域内的以
,其中C为在函数定义域内的以![]() 为聚点的一个点集,例如通过
为聚点的一个点集,例如通过![]() 的一条曲线。按此方式,极限
的一条曲线。按此方式,极限![]() 不存在。
不存在。
2、找出两种方式:![]() 与
与![]() ,使
,使
![]() ,
,
![]() ,
,
且![]() ,则二重极限
,则二重极限![]() 不存在。
不存在。
例1、讨论极限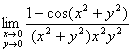 。
。
解:因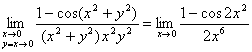
![]() 不存在。
不存在。
故原极限不存在。
例2、讨论极限![]() 。
。
解:因为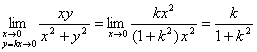 ,其值因k而异,故原极限不存在。
,其值因k而异,故原极限不存在。
例3、讨论极限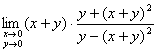
解:因为
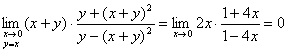 ,
,
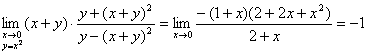 。
。
答:
由于二重极限定义中动点![]() 趋向于点
趋向于点![]() 的方式是任意的,因而平面上的点P趋向于P0的方式可有无穷多,比起一元函数的极限只有左、右两个单侧极限来说,要复杂得多。
的方式是任意的,因而平面上的点P趋向于P0的方式可有无穷多,比起一元函数的极限只有左、右两个单侧极限来说,要复杂得多。
求函数![]() 的二重极限常用的方法有:
的二重极限常用的方法有:
(1)利用连续的定义及初等函数的连续性。如果![]() 是
是![]() 的连续点,那末便有
的连续点,那末便有
![]() 。
。
(2)利用极限的性质(如四则运算,夹逼定理)。
(3)先用观察的方法,猜测数A可能是函数![]() 的极限,然后用二重极限定义去验证。
的极限,然后用二重极限定义去验证。
(4)消去分子分母中极限为零的因子。
(5)转化成一元函数的极限问题,利用一元函数中的已知极限。问题9:我们把先后两次求出的极限![]() 或
或![]() (1)称为二次极限(也称累次极限),它们与二重极限
(1)称为二次极限(也称累次极限),它们与二重极限![]() (2)是否为一回事?
(2)是否为一回事?
答: 不是一回事.二重极限(2)是点![]() 以任意方式趋于
以任意方式趋于![]() 时二元函数
时二元函数![]() 的极限;而累次极限(1)是点
的极限;而累次极限(1)是点![]() 沿特殊方式——折线
沿特殊方式——折线![]() 和
和![]() (或
(或![]() 和
和![]() )趋于
)趋于![]() 时两个一元函数的极限(读者自绘草图帮助理解),而且这是不一样的两回事,并不是一般与特殊的关系(折线上的点可能位于邻域之外).例如,
时两个一元函数的极限(读者自绘草图帮助理解),而且这是不一样的两回事,并不是一般与特殊的关系(折线上的点可能位于邻域之外).例如,
例1、设![]()
![]() ,其两个累次极限
,其两个累次极限
![]() ;
;
但令![]() ,即点
,即点![]() 沿任意直线
沿任意直线![]() 而趋于原点(0,0)时,
而趋于原点(0,0)时,
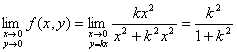 ,
,
它随k取不同的值,可见上述二重极限不存在;
例2、设![]() ,则因为
,则因为
![]() ,
,
∴![]() ,
,
但![]() 不存在,而
不存在,而![]() ,从而累次极限
,从而累次极限![]() 不存在.同理另一个累次极限也不存在.
不存在.同理另一个累次极限也不存在.
由上述可见,二重极限与二次极限没有必然的关系,即使两个累次极限都存在且相等也不能保证二重极限存在,反之亦然,一般而言,求累次极限容易一些,可借用一元函数求极限的各种方法,但这代替不了二重极限.
它们之间的关系表现在:当![]() ,
,![]() ;
;
这两个一元函数连续的等式不能保证二元函数连续的下述等式成立:
![]()
即是说,二元函数连续的定义是建立在二重极限的基础之上,因此,对每一个变量连续只相当于一种特定方式的极限存在(如对![]() 连续,相当于
连续,相当于![]() ),它不能代替所有
),它不能代替所有![]() 的方式下极限都存在。因此,我们不能从
的方式下极限都存在。因此,我们不能从![]() 分别对每个变量
分别对每个变量![]() 与
与![]() 都连续而得出
都连续而得出![]() 一定是连续的结论。
一定是连续的结论。
例1、设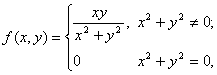 ,则易见
,则易见
![]() .
.
但![]() 在(0,0)处的二重极限不存在,从而此二元函数在点(0,0)不连续.
在(0,0)处的二重极限不存在,从而此二元函数在点(0,0)不连续.
反之则成立.这是一般与特殊的关系.事实上,在![]()
![]() 中取特殊方式
中取特殊方式![]() 或
或![]() ,易知:
,易知:
答: 对一元函数来说,可导必连续。但在多元函数中,这一重要关系不再保持,连续与可导之间没有必然的联系。也就是说连续未必可导;可导也未必连续。
例如,函数![]() 在点(0,0)处连续,但它在点(0,0)处的两个偏导数都不存在。而函数
在点(0,0)处连续,但它在点(0,0)处的两个偏导数都不存在。而函数
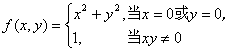
在点(0,0)处有
![]()
答:
可微必连续,但反之不真。
可微必连续,教材中已有证明。反之不真,举例说明如下:
函数

在点(0,0)处是连续的,因为当![]() 时,有
时,有
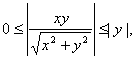
故有![]()
又![]() 在点(0,0)处可导,且
在点(0,0)处可导,且![]() ,但
,但![]() 在点(0,0)处是不可微的,因为
在点(0,0)处是不可微的,因为
![]() =
=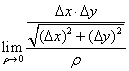
=![]()
![]()