答:
(1)满足微分方程的函数,称为该方程的解;
(2)对![]() 阶微分方程,包含了
阶微分方程,包含了![]() 个任意独立常数的解
个任意独立常数的解![]() 称为微分方程的通解;
称为微分方程的通解;
(3)对于![]() 阶微分方程,为了从通解中找到所需要的解,需要附加
阶微分方程,为了从通解中找到所需要的解,需要附加![]() 个初始值条件,即
个初始值条件,即
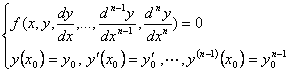
这样的定解条件称为初值条件(initial condition),上述问题就称为初值问题.或者Cauchy问题;
满足微分方程, 并且适合定解条件的解称为微分方程的特解。答:
微分方程的存在唯一性定理:
对一阶初值问题: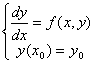 ,若二元函数
,若二元函数问题3:一阶可积微分方程有几种类型?
(1)可分离变量型:形如![]() ,或
,或![]() 。
。
例1:解方程![]() .
.
解:将方程化为![]()
积分得到通解![]() .
.
(2)可化为可分离变量型的方程
I.齐次方程:![]() , 作代换
, 作代换![]() ,则
,则![]() ,即
,即
![]() ,
,
将这类方程化成了可变量分离的方程。
例2:求此曲线![]() ,使其上每点
,使其上每点![]() 的法线平分过这点的水平线与矢径所交之角。
的法线平分过这点的水平线与矢径所交之角。
解: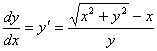 .令
.令![]() ,代入方程得
,代入方程得
![]() ;
;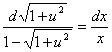
即![]()
![]()
![]() 。
。
这是抛物线。
II.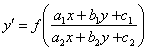 ,先作变量
,先作变量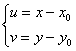 将其变成关于
将其变成关于![]() 的零齐方程,
的零齐方程,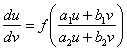 。
。
III.![]() ,令
,令![]() ,
,![]() ,
,![]() ,代入
,代入![]() 得
得![]() ,即
,即![]() 。
。
(3)一阶线性微分方程![]()
常数变易法:先求解![]() ,得
,得![]() ,再设
,再设![]() 的解为
的解为![]() ,代入方程得
,代入方程得
![]() ,
,
解得![]() ,
,![]() 的通解为
的通解为
![]() 。
。
例3:解方程![]() .
.
解:先求解![]() ,得
,得![]() ,再设
,再设![]() 的解为
的解为![]() , 代入得
, 代入得![]() ,即
,即![]() ,故题解为
,故题解为![]() .
.
(4)贝努利方程![]()
两边同乘![]() ,得
,得![]() ,再设
,再设![]() ,代入方程得
,代入方程得
![]() ,化成了一阶线性微分方程。
,化成了一阶线性微分方程。
(5)全微分方程![]()
其中![]() 与
与![]() 连续可微的函数.若满足可积性条件:
连续可微的函数.若满足可积性条件:
![]()
则称该方程是全微分方程。
例4:解方程![]() .
.
解:是一个全微分方程.下面用三种方法求解这个方程.
解法1:线积分法。
解法2:凑全微分法,将方程中各项重新组合为
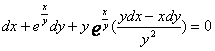 ,
,
即![]()
![]() ,
,
答:
一般情况下,求解高阶方程更加困难.处理高阶方程的思路之一是设法降低方程的阶.在这里,仅讨论二阶方程
![]()
的几种右端函缺缺变量的情形进行讨论.
(1)![]() 类型
类型
令![]() ,
,![]() ,方程变成:
,方程变成:![]()
这是一阶方程,有可能求解。
例1:解方程![]() .
.
解:令![]() ,代入方程,则原方程化为:
,代入方程,则原方程化为:![]()
由此解出![]() ,于是原方程的通解为
,于是原方程的通解为![]() .
.
(2)![]() 类型
类型
令![]() ,
,![]() ,
,
代入方程得![]() .
.
于是得到一个关于未知函数![]() 和自变量
和自变量![]() 的一阶方程.
的一阶方程.
例2:解方程![]() .
.
解:令![]() ,
,![]() ,代入方程得到
,代入方程得到
![]()
![]() 即
即![]() .
.
两端积分得到![]() .即,
.即,![]()
分离变量,将上式改写成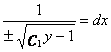
答:
![]() 阶线性微分方程的一般形式为
阶线性微分方程的一般形式为
![]() ,
,
其中![]() 以及
以及![]() 都是区间
都是区间![]() 上的已知连续函数.当
上的已知连续函数.当![]() 时,变成相应的齐次方程:
时,变成相应的齐次方程:
![]()
为简便计,记:![]() 阶导数符号
阶导数符号![]() ,及多项式微分算子:
,及多项式微分算子:
![]() ,
,
这样![]() 阶线性齐次微分方程可表成:
阶线性齐次微分方程可表成:![]() ,
,
![]() 阶线性非齐次微分方程可表成:
阶线性非齐次微分方程可表成:![]() 。
。
(1)若![]() 都是方程
都是方程![]() 的解,则对任意常数
的解,则对任意常数![]() ,
,
函数![]() 也是该方程的解。
也是该方程的解。
(2)方程![]() 的所有解构成一个
的所有解构成一个![]() 维线性空间,其中任意
维线性空间,其中任意![]() 个线性无关的解,
个线性无关的解,![]() ,构成该空间的一组基。
,构成该空间的一组基。
(3)非齐次方程![]() 之解
之解
答:
观察待定法。
设有二阶齐次方程:![]() ,
,
若己知二阶齐次方程![]() 的一个特解
的一个特解![]() ,用变动任意常数法,设
,用变动任意常数法,设![]() ,代入方程可求出另一个无关特解。
,代入方程可求出另一个无关特解。
例:![]()
解:可观察出一个解:![]()
利用侍定函数法求第二个特解(变动任意常数法):
解是