答：

函数的导（函）数没有第一类间断点。

反之，如果函数有第一类间断点，那么函数一定不存在原函数。例如，函数

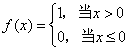
答：

在各种高等数学的教材中，关于函数的不定积分有以下三种定义：

（1）函数的原函数的全体。

（，其中,是任意函数）d

（2）函数的原函数的一般表达式。

（其中，是任意函数）

二者所指的对象“原函数的全体”与：“原函数的一般表达式”基本相同。但是，他们着眼点不同。（1）着眼于原函数的全体，即原函数的集合，即

（2）着眼于原函数的一般表达式，即原函数的形式，即

前者指的是集合，后者指的是原函数的形式。

因为读者在中学已熟知了集合概念，所以教材中采用“原函数的全体”定义不定积分。

因此，两个不定积分相等，实质是原函数的集合相等。例如

不一定。例如，函数，定义域是，是函数在内的一个原函数，而

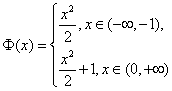
也是函数在内的一个原函数，但是，

在内并不是常数。

函数的一个原函数不能说它是的不定积分，的全体（或所有）原函数才是它的不定积分，这是两个不同的概念。初学者经常将任意常数丢掉而写成是错误的。

答：

分部积分公式是由两个函数乘积的导数公式反转过来的，即

它表示等号两端的原函数集合相等，这种形式的分部积分公式，既便于记忆，又便于应用。

分部积分法是求不定积分不可缺少的方法之一，例如，求对数函数的不定积分必须使用分部积分公式。由此可见，分部积分法的重要性。

应用分部积分公式关键是把被积表达式改写为与的乘积。改写的原则是要比简单，即不定积分更好求。甚至可应用不定积分表中的公式直接得到结果，应用分部积分公式的困难就在此，技巧也在此，例如

＝

显然，要比简单，而的不定积分由不定积分表中的公式可直接得到结果，

应用分部积分公式还能得到一些有用的递推公式，例如，求不定积分

必须使用分部积分公式，有递推公式

其中

　答：

利用以上公式计算不定积分就是所谓的分部积分法。在利用以上公式计算不定积分时，要注意以下三点：

1）要容易求得；

2）比容易计算，所以找到后要对前面这两个积分进行评估；

3)因为，所以的选取不唯一，我们可利用这点来简化计算。

例1：计算时，我们可以取

（1）

也可以取

（2）

在第一种取法中，不容易求得，即我们看不出比简单，这样使用分部积分法也就没有什么意义（不能简化计算）。

再来看第二种取法，很容易求得，，显然这样变化后，得次数增加了。接下来我们要评估和的难易程度。因为，所以

用拆项法很容易计算出此不定积分，因此，第二种取法比较合适。

还必须注意到的选取是不唯一的，我们可以选取适当的进一步简化计算，例如在第二种取法中，如果选取，则有

这样使得更加简单。

例2：计算（为非零常数）；

解：令，则

（1）

左右两边的积分计算难易程度基本上没什么变化，所以我们换个方向，

令，则

（2）

得

　　答：

分部积分公式是有两个函数乘积的导数公式反转过来的，即

它表示等号两端的原函数集合相等，分部积分法是求不定积分不可缺少的的方法之一。这一方法多用于求被积函数为两个函数（包括常数函数）乘积形式的的不定积分。应用分部积分公式关键是如何选择和（）。其原则是：设法使比简单，而也不比复杂，即要比简单。一般来说，没有一定之规，具体问题具体分析。但对几种常见类型不定积分，还是有规律可循的。下面介绍“对反幂三指”方法。

这里，“对”是对数函数；“反”是反三角函数；“幂”是幂函数；“三”是三角函数；“指”是指数函数。

“对反幂三指”方法：如果在原来的不定积分的被积函数中是这五种函数中任何两种的乘积形式，我们选择位于“对反幂三指”五字中前面那个字所代表的函数作为，余下的表达式作为。

得到的结果

是正确的。但将不定积分看作是一个数，进行运算是错误的。因为不定积分不是一个数而是被积函数的原函数集合，所以上述等式是两个函数集合相等，已知

Ⅰ

虽然用分部积分所得的不定积分与所求的不定积分类似，未使新的不定积分简化，但是，若再次使用分部积分方法，有

（Ⅰ）

把右端末项Ⅰ移到左端，有

﹡

Ⅱ

（Ⅱ）

把右端末项Ⅱ移到左端，有0=1﹡﹡

两题运算用到了将等号右端出现的Ⅰ与Ⅱ分别移到等号左端，得到最后结果﹡与﹡﹡。但是，前例移项得到的﹡式是正确的。后例移项得到的﹡﹡式是错误的。因为，两端仅差一个常数，从求不定积分运算来说丝毫没有进展，即若，，则，，有的任意性，则原函数集合

，

所以，得出0=1，遇到这种情况不能采取移项办法，正确作法：

Ⅱ

此公式用第一类换元法（凑微分法）很容易得出。利用好这一公式可以大大简化许多积分计算题。

例1：计算

对于这一积分，我们可以先求分母的导数，，显然此题不能直接利用以上公式，但我们可以把分子化为，用拆项法得

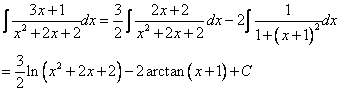
例2：计算

这个积分，被积函数不是分式（或说分母为1），也不能直接利用以上公式，我们把看成分子分母同乘以可得，对分母求导

导数刚好是分子，所以

例3：计算

这个积分，也不能直接利用以上公式，我们先对被积函数的分子分母同乘，

然后对分母求导，而分子可化为，因此

例4：计算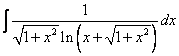

在计算此积分时，一般的思路是用换元法去根号、去对数，但这样的计算比较繁。如果我们先考虑一下求导结论

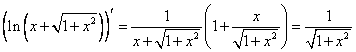
就容易发现此积分用公式计算很简洁