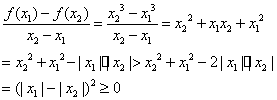答:
一般有两种情形:
1、讨论分段函数在分段点处的可导性。
例:讨论函数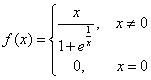 在z=0 处是否可导。
在z=0 处是否可导。
解:由于![]()
![]() 所以要分别讨论函数f(x)在x=0处的左右导数。
所以要分别讨论函数f(x)在x=0处的左右导数。
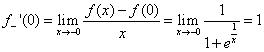 ,
,
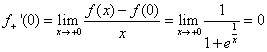 。
。
左右导数不相等,故f(x)在x=0处不可导。
2、讨论可导性未给出的抽象函数在某点处的导数。
例:已知![]() ,
,![]() 在
在![]() 处连续,
处连续,![]() 。求
。求![]() 。
。
解:由于抽象函数![]() 在
在![]() 处的可导性未知,所以要用定义求
处的可导性未知,所以要用定义求![]() 。
。
![]() 。
。
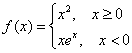 ,问f(x) 在其定义域内是否处处连续?处处可导?研究下述做法是否正确。
,问f(x) 在其定义域内是否处处连续?处处可导?研究下述做法是否正确。
解:由于
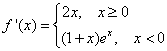 ,所以f(x)在其定义域内是否处处可导,当然处处连续。
,所以f(x)在其定义域内是否处处可导,当然处处连续。
答:
上述做法,对于x>0和 x<0 时,利用导数公式和运算法则,结果是正确的。但在 x=0 处,函数是否可导,应该从定义考察(易知![]() 在x=0 处连续)。因为
在x=0 处连续)。因为
![]() ,
,
![]() ,
,
即![]() 不存在,所以
不存在,所以![]() 在x=0处不可导。
在x=0处不可导。
问题3:设函数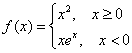 ,讨论f(x)在x=0处是否可导时,有人用下面的方法:由
,讨论f(x)在x=0处是否可导时,有人用下面的方法:由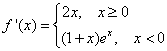 ,得
,得
![]() ,
,![]() ,
,
上述解法是对的。根据导函数的左、右极限都存在,但不相等得出结论“![]() 在x=0处不可导”是对的。
在x=0处不可导”是对的。
不可以。例如对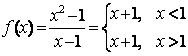 有
有![]() ,
,
但是![]() 在
在![]() 处无定义,即不连续,自然不可导。正确的结论应该是:如果
处无定义,即不连续,自然不可导。正确的结论应该是:如果![]() 和
和![]() 都存在且相等,又
都存在且相等,又![]() 在
在![]() 处连续,则
处连续,则![]() 在
在![]() 可导。
可导。
答:
关键是搞清复合关系,从外层到里层一层层地求导,不要漏层。当所给的函数既有四则运算又有复合运算时,应根据函数的表达式结构,确定先用四则运算还是先用复合函数求导法则。
不同。![]() 是复合函数
是复合函数![]() 对自变量
对自变量![]() 的导数,
的导数,![]() 则是函数
则是函数![]() 对
对![]() (
(![]() )的导数,再将
)的导数,再将![]() 换成
换成![]() 。
。
1、方程两边对x求导数,要记住y是x的函数。
2、利用微分形式不变性,在方程两边求微分,然后解出![]() 。
。
1、化为指数函数:
2、取对数函数:
1、直接法:求出函数的1—3阶或4阶导数后,分析所得结果的规律性,写出n阶倒数。
2、利用已知的高阶导数公式,通过四则运算,求n阶导数。
例:![]() ,则
,则![]() 。
。
3、利用递推公式求n阶导数。
例:设![]() ,求
,求![]() 。
。
解:因![]() ,由此得
,由此得
![]() 。
。
两边求导数得:
![]() ,
,
![]() ,
,
......,
![]() ,
,
1、概念上有本质的不同。函数![]() 在
在![]() 点的导数
点的导数![]() 是函数
是函数![]() 在x点关于自变量的变化率,反映了函数y在x点随自变量变化的快慢程度。微分
在x点关于自变量的变化率,反映了函数y在x点随自变量变化的快慢程度。微分![]() 是在以
是在以![]() 和
和![]() 为端点的微小区间上以函数y在x点的变化率
为端点的微小区间上以函数y在x点的变化率![]() 代替该小区间上任意点处的变化率后所得到的线性函数的增量(
代替该小区间上任意点处的变化率后所得到的线性函数的增量(![]() 的线性主部)。
的线性主部)。
2、当x给定时,导数![]() 是一个常数,微分
是一个常数,微分![]() 是
是![]() 时的无穷小。
时的无穷小。
1、函数![]() 在x可导与可微是等价的。
在x可导与可微是等价的。
2、![]() 表明函数
表明函数![]() 的导数
的导数![]() 等于函数的微分
等于函数的微分![]() 与自变量的微分
与自变量的微分![]() 之比。
之比。
要注意三个方面:
1、对于![]() 型或
型或![]() 型未定式才能直接使用洛必达法则。
型未定式才能直接使用洛必达法则。
2、使用洛必达法则求极限时,应及时化简(例如:通过代数运算、三角恒等式约去公因子,分离极限不为零的因子,利用等价无穷小替换,变量代换等)。
3、洛必达法则的条件是充分的,不是必要的,因此,当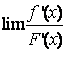 不存在(不含
不存在(不含![]() 的情形)时,并不能断定
的情形)时,并不能断定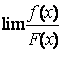 也不存在,只是这时不能使用洛必达法则,而需要使用其它方法讨论。
也不存在,只是这时不能使用洛必达法则,而需要使用其它方法讨论。
1、构造函数![]() 或
或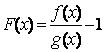 ;
;
2、考察![]() 在区间I及其端点处的连续性;
在区间I及其端点处的连续性;
3、求出![]() ,由
,由![]() 的符号判断F(x)在区间I的单调性;
的符号判断F(x)在区间I的单调性;
一个根本的原则是:在题设条件中若函数![]() 二阶或二阶以上可导,就将
二阶或二阶以上可导,就将![]() 在指定点展开成泰勒公式。
在指定点展开成泰勒公式。
例1、设C为实数,函数![]() 满足:
满足:![]() ,
,![]() 。求证:
。求证:![]() ,
,![]() 。
。
证明:由泰勒公式有
![]()
![]()
两式相加得
![]()
两式相减得
![]()
当![]() 时,
时,![]() ,
,![]() ,于是有
,于是有
![]() ,
,![]() 。
。
例2、设![]() ,且
,且![]() 。求证:
。求证:![]() 。
。
证明:因为![]() 连续且可导,故由由
连续且可导,故由由![]() 知
知![]() ,
,![]() 。由泰勒公式有
。由泰勒公式有
![]()
![]() 在
在![]() 与
与![]() 之间。
之间。
罗尔定理三个条件都是重要的,如果缺少了其中的任何一个,定理的结论就不一定成立。
例如,函数
![]()
虽然函数![]() 在区间[0,1]上满足罗尔定理的条件(2)和(3),但它不满足条件(1),即
在区间[0,1]上满足罗尔定理的条件(2)和(3),但它不满足条件(1),即![]() ,因此在区间(0,1)内不存在点
,因此在区间(0,1)内不存在点![]() ,使
,使![]()
函数![]() 在区间
在区间![]() 上满足罗尔定理的条件(1)和(3),但它不满足条件(2),即在点
上满足罗尔定理的条件(1)和(3),但它不满足条件(2),即在点![]() 处函数
处函数![]() 不存在导数,因此在区间(0,1)内不存在点
不存在导数,因此在区间(0,1)内不存在点![]() ,使
,使![]()
函数![]() 显然在区间
显然在区间![]() 上满足罗尔定理的条件(1)和(2),但它不满足条件(3),即
上满足罗尔定理的条件(1)和(2),但它不满足条件(3),即![]() 因此在区间(0,1)内不存在点
因此在区间(0,1)内不存在点![]() ,使
,使![]()
然而罗尔定理的条件是充分的。即存在这样的函数,罗尔定理的条件均不满足,但是在函数的定义域内确存在点![]() ,使
,使![]() 例如,函数
例如,函数
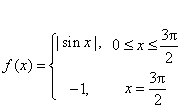
函数在![]() 不连续,点
不连续,点![]() 是函数的角点,且
是函数的角点,且![]() 即罗尔定理的三个条件都不满足,但是在区间
即罗尔定理的三个条件都不满足,但是在区间![]() 内确存在点
内确存在点![]() ,使得函数在点
,使得函数在点![]() 处有
处有![]()
答:
(1)基本思想:我们知道,拉格朗日中值定理的条件较罗尔定理的条件少一个端点的函数值相等,因此不能直接运用罗尔定理来证明拉格朗日定理。如果能够构造一个辅助函数![]() ,使罗尔定理的三个条件都能得到满足,那么在区间
,使罗尔定理的三个条件都能得到满足,那么在区间![]() 内寻求点
内寻求点![]() 使之
使之![]() 的问题就转化为在区间
的问题就转化为在区间![]() 内寻求点
内寻求点![]() 使之
使之![]() 。
。
(2)具体作法:由于![]() ,不妨设
,不妨设![]() ,则
,则![]() 是曲线上连接点
是曲线上连接点![]() 和点
和点![]() 的割线斜率。因此过
的割线斜率。因此过![]() 两点的直线方程为
两点的直线方程为
![]() .
.
由于曲线方程![]() 与
与![]() 两点的直线在点
两点的直线在点![]() 处的函数值相等,所以用曲线方程
处的函数值相等,所以用曲线方程![]() 减去割线方程就得到我们要作的辅助函数,即
减去割线方程就得到我们要作的辅助函数,即
![]() .
.
如果对函数![]() 和
和![]() 分别应用拉格朗日中值定理,则得
分别应用拉格朗日中值定理,则得
![]()
从而有
![]()
不难看到,这里的![]() 未必相同。不能满足公式中的中间值
未必相同。不能满足公式中的中间值![]() 的要求。这就是柯西定理的优越性。
的要求。这就是柯西定理的优越性。
只须展开至分子及分母分别经过化简后系数不为零的阶数即可。如
求极限![]() 。
。
![]() (*)
(*)
若用罗必塔法则则是相当烦琐的。下面用泰勒公式方法与等价无穷小方法相结合来考虑。
![]()
由泰勒公式
![]()
于是
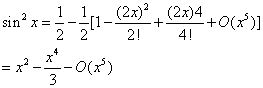
将(*)式中分子上的![]() 用上式代,而分母的
用上式代,而分母的![]() 用
用![]() 代,这样
代,这样
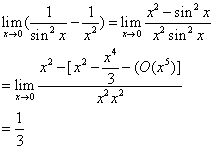
应指出的是,在证明不等式所用的余项为拉格朗日形式而在求极限所用余项为皮亚诺形式。
问题19:若函数f(x)在区间(a,b)内有连续的导函数f'(x)。对于区间(a,b)内任何一点![]() 能否从此区间中找到另外两点
能否从此区间中找到另外两点![]() 使之满足于
使之满足于
![]()
解答:一般地说,不可以。例如研究函数
![]()
它对于![]() 就找不到所需的
就找不到所需的![]() 使
使
![]()
事实上,![]() 而当
而当![]() 时,
时,