答:
函数的定义域和对应关系(或对应法则)是确定函数的两个基本要素,只要它们给定,函数就完全确定。
常见的有解析式、几何图像、函数表等几种形式,有的还可以用语言文字叙述给出。下面是两个用语言文字给出的函数
(1) x设y 是实数, y是不超过 x 的最大整数。
(2) Dilichlet函数: ![]()
答:
两个函数,如果它们的定义域相同、对应关系相同(给出的形式不同,但对于自变量的每一个值,相应的两个函数值都相等),则称两个函数相等,或者说它们是同一函数。
例如函数 (1)![]() , (2)
, (2)![]() , (3)
, (3)![]() .
(1) 和(2)的定义域均为|x|>1 ,(3)x>0的定义域为 ,显然(1)
和(2)是相同的函数,(3)和它们不同。
函数的表示只与定义域和对应关系有关,而与用什么字母表示无关。这个性质特别重要,常利用这个性质,由f[g(x)]的表达式来求函数f (x)的解析表达式.
.
(1) 和(2)的定义域均为|x|>1 ,(3)x>0的定义域为 ,显然(1)
和(2)是相同的函数,(3)和它们不同。
函数的表示只与定义域和对应关系有关,而与用什么字母表示无关。这个性质特别重要,常利用这个性质,由f[g(x)]的表达式来求函数f (x)的解析表达式.
例如: 设![]() ,
,![]() ,求f (x)
,求f (x)
解:令 ![]() ,
,![]() ,则得
,则得![]() =
=![]() ,
即 .
,
即 . ![]()
![]()
答:
有的函数在整个定义域上不能由一个解析式表达,而在定义域的不同段上由不同的解析式给出,这样的函数称为分段函数。例如 ![]()
是分段函数,当![]() 时,由解析式y=x2+1 计算y 值,当
时,由解析式y=x2+1 计算y 值,当![]() 时,由解析y=x 计算y 值。
注意分段函数是用分段解析给出的函数,不能错误地认为它是几个函数。
时,由解析y=x 计算y 值。
注意分段函数是用分段解析给出的函数,不能错误地认为它是几个函数。
答:
设函数y=f(u),u=ψ(x),它们的定义域分别为D1和D,后者的值域为D2。它们两个能够复合的条件是ψ(x)的函数值全部或部分地含在f(x)地定义域内,即D1ID2≠φ。这是两个函数复合必须具备的条件。
复合函数的定义域是取得函数值![]() 中所有x值。记成D0,显然
中所有x值。记成D0,显然![]() 。若
。若![]() ,则
,则![]() 。若
。若![]() ,
,![]() 且
且![]() 则 ,
则 ,![]() 且
且 ![]() 。
。
例如,设![]() ,
,![]() ,
,![]() ,求y 作为 x 的复合函数。
首先,函数
,求y 作为 x 的复合函数。
首先,函数![]() 的值域为u>-1 ,它于函数
的值域为u>-1 ,它于函数![]() 定义域的公共部分为u>0 和 -<u<0。于是,两个函数可以复合。
定义域的公共部分为u>0 和 -<u<0。于是,两个函数可以复合。
确定复合函数的定义域。由 ![]() 可知,当u>0 时,
可知,当u>0 时, ![]() ,当-1<u<0 时,
,当-1<u<0 时,![]() 。
从而得到复合函数?
。
从而得到复合函数?![]() ,
,![]() 或
或![]() 关于复合函数,要提及的是,利用复合运算可将复杂函数分解成比较简单的函数,这对复杂函数微分运算是十分重要的。
关于复合函数,要提及的是,利用复合运算可将复杂函数分解成比较简单的函数,这对复杂函数微分运算是十分重要的。
答:
(1)是同一函数。(参见问题2)
(2)y=f(x) 与x=f-1(x) 在同一坐标系中的图象相同(重合);
y=f(x)与y=f-1(x) 在同一坐标系中的图象关于直线y=x 对称.
注意:正确理解该几何表现对后续内容的学习极为重要。例如对第二章“反函数求导法则”就可以从几何上作直观的理解。
答:
上述解法还是有一定正确性的,但考虑问题不够全面.
事实上,当x≠k(k=0,±1,±2 ...) 时,虽然![]() 取虚数值,但若考虑x-|x|=0
取虚数值,但若考虑x-|x|=0
![]() 还是有意义的,其值为零.故当x≥0 时,x-|x|=0,函数有意义,于是所求函数的定义域为x≥0及 x=-k(k=1,2..)
还是有意义的,其值为零.故当x≥0 时,x-|x|=0,函数有意义,于是所求函数的定义域为x≥0及 x=-k(k=1,2..)
答:
偶延拓:设函数y=f(x) ,x∈[0,a]作函数
![]()
则F(x) 是[-a,a] 上的偶函数,且在[0,a] 上,F(x)=f(x) ,称F(x) 是f(x) 的偶延拓。
奇延拓:设函数 y=f(x),x∈[0,a]作函数
![]()
则 F(x)是[-a,a] 上的奇函数,且在[0,a] 上,F(x)=f(x) ,称F(x)是f(x) 的奇延拓。
周期延拓:设函数y=f(x) ,x∈[a,b]作函数
![]()
则F(x) 是以b-a 为周期的周期函数,在[a,b] 上,F(x)=f(x),称F(x) 是f(x) 的周期延拓。
函数的奇偶分解:
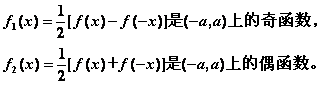
答:
不一定有最小正周期。尽管我们所学的周期函数一般都有最小正周期,但周期函数不一定有最小正周期。
例如:狄利克雷(Dirichlet)函数
![]()
是一个以任何正有理数为周期的函数,因为正有理数没有最小正数,故狄利克雷函数无最小正周期。
除此之外,最简单的常数函数f(x)=C 也是周期函数,任何正实数都是其周期,同样不存在最小正周期。
答:
常用三种办法判定函数的周期性:
= 1 \* GB2 ⑴周期函数的定义域一定是既无上界有无下界的,所以如果发现函数的定义域有上界或有下界,那么肯定不是周期函数。
= 2 \* GB2 ⑵假设函数f(x) 是周期函数,那么方程f(x)=0 或(方程 f(x)=k0,k0为常数)只要有根,则根的分布一定具有周期性。如果根的分布不具有周期性,那么肯定不是周期函数。
= 3 \* GB2 ⑶把 固定为某个x0 ,解方程f(x0+l)=f(x0) ,找出方程的全部解l=ln(1,2,3...) ,再逐个检查ln是否对定义域内所有 x 满足f(x+l)=f(x)满足则是周期函数,否则不是。
答:
不对,因为越来越接近并不意味着无限的接近。应该说:“当n 充分大时,xn 与a之差的绝对值可以小于预先给定的任意正数ε ”,或者说“当n 越来越大时,xn 越来越无限地接近于 a”。例如:![]() ,但|yn-0|=yn 并不是单调减少的,说yn 越来越接近于0也不准确。
,但|yn-0|=yn 并不是单调减少的,说yn 越来越接近于0也不准确。
答:
一般不是的。由数列{xn} 收敛可以推出数列{|xn|} 收敛,因为有||xn|-|a||≤|xn-a| 的三角不等式,但反过来不行,例如 xn=(-1)n就是一个例子。如果数列 {|xn|}发散,则数列 {xn}发散,反过来也不成立。
答:
不对。因为极限的四则运算法则是由条件的,两项之商的极限等于这两项的极限的商要求分母的极限不等于0。因此当a≠0 时正确,但当a=0 时不正确,作为一个命题,条件是不充分的,因此不对。
事实上当a=0 时极限![]() 可以存在,也可以不存在,即使存在也不一定就等于1。例如
可以存在,也可以不存在,即使存在也不一定就等于1。例如![]() 就有
就有![]() 不存在。又如
不存在。又如![]() ,而
,而![]() 。
。
答:
证明数列无界最常用的方法就是找出它的一个无穷大子列。所谓子列,就是从原来数列中抽取的无限项组成并按原来的先后次序排列的新的数列,例如{x2n} 、{x2n-1} ![]() 、
、 ![]() 都是 {x2n} 的子列。可以推出这样的定理:数列{x2n} 无界的充分必要条件是{x2n} 存在无穷大子列。有理这个定理,我们要证明数列
都是 {x2n} 的子列。可以推出这样的定理:数列{x2n} 无界的充分必要条件是{x2n} 存在无穷大子列。有理这个定理,我们要证明数列![]() 无界,只要找到一个子列如
无界,只要找到一个子列如![]() ,再用无穷大的定义证明它是无穷大量即可。
,再用无穷大的定义证明它是无穷大量即可。
答:
由教材我们知道:如果对数列{xn} 有![]() ,则{xn} 的任何子列都以 a为极限。因此,要证明一个数列发散,也就是不收敛,我们只要找到它的一个子列发散或者两个子列不以同一个数为极限即可。这样的数列是有目的构造出来的。
,则{xn} 的任何子列都以 a为极限。因此,要证明一个数列发散,也就是不收敛,我们只要找到它的一个子列发散或者两个子列不以同一个数为极限即可。这样的数列是有目的构造出来的。
例如:针对数列![]() ,我们把一般项具体化试一试就发现它的偶数项
,我们把一般项具体化试一试就发现它的偶数项![]() 是发散的,于是找到了一个发散的子列,可以证明原数列发散。
是发散的,于是找到了一个发散的子列,可以证明原数列发散。
又如针对数列![]() ,我们也把一般项具体化试一试,容易发现
,我们也把一般项具体化试一试,容易发现 ![]() ,
,![]() ,于是找到了两个子列子列,它们收敛于不同的数,也就证明了原数列发散。
,于是找到了两个子列子列,它们收敛于不同的数,也就证明了原数列发散。
答:
证明数列不为无穷大最常用的方法就是找出它的一个收敛的子列。因为若 {xn} 为无穷大,则它的任何子列都是无穷大量。所以,若某个子列收敛,即该子列不是无穷大量,从而可以推出原数列也不是无穷大量。例如要证明![]() 不是无穷大,只要找到他的子列
不是无穷大,只要找到他的子列![]() ,并说明该子列是收敛到0的即可。
,并说明该子列是收敛到0的即可。
答:
对的。我们可以证明如下一般性结论:
设 ![]() 、
、![]() 都是
都是 ![]() 的子列,若
的子列,若![]() ,
,![]() 且
且![]() ,则
,则![]() 。
。
证:由已知,任给 ε>0,存在k1 >0,当k>K1 时总有![]() ;
;
同样存在K2>0 ,当k>K2 时总有![]() 。
这样我们可以取
。
这样我们可以取 ![]() ,当 n>N 时,若
,当 n>N 时,若![]() ,则有某个 ,于是
,则有某个 ,于是 ![]() ;若
;若![]() ,则必有
,则必有![]() ,即有某个
,即有某个![]() ,于是也有
,于是也有 ![]() 。所以
。所以![]() 成立。
成立。
答:
= 1 \* GB2 ⑴{xn} 、{yn} 都收敛,由极限四则运算法则可以推出{xnyn} 收敛;
= 2 \* GB2 ⑵{xn} 、{yn} 其中一个收敛,另一个发散, {xnyn}的收敛性没有确定的结论,问题是 {xn}、{yn} 中收敛的一个可能收敛到0,否则可确定 {xnyn}必发散(这可以用反证法证明)。例如:![]() ,则{xnyn} 收敛,而
,则{xnyn} 收敛,而![]() 时,{xnyn} 发散。
时,{xnyn} 发散。
= 3 \* GB2 ⑶ {xn}、 {yn}两个都发散, {xnyn}的收敛性也没有确定的结论。例如: xn=yn=(-1)n,则 {xnyn}收敛,而 xn=(-1)n时,{xnyn} 发散。
答:
以![]() 为例进行分析。
为例进行分析。
极限的概念是刻划在点 x0 附近有定义的函数f(x) ,当x 充分靠近 x0 时,函数值f(x) 可以任意靠近常数 A,这样的变化趋势。函数的这种变化趋势如何用严格的数学语言精确描述呢?度量x 与 x0 的靠近程度就要用|x- x0| ,而度量 f(x)和常数A 的靠近程度就要用|f(x)-A| 。 f(x)可以任意靠近常数A ,即对于任意的正数ε , |f(x)-A|< ε成立,其条件是 x充分靠近 x0 ,即存在正数 δ,有 0<|x- x0 | < δ。极限定义 ![]() 要注意以下几点:
要注意以下几点:
(1)f(x) 在点x0 附近有定义,并不要求它在x0 点有定义,换言之, f(x)在点x0 可有定义也可没有定义。
(2)正数 ε的任意性是对所有正实数而言,其实,若对小正数ε ,能存在δ > 0 ,当 0< |x- x0 |< δ时,有 |f(x)-A|< ε,那么对大正数ε ,照样还是这个 δ,当前一个不等式成立时,后一个不等式自然成立。既然如此,可否限制ε ,比如说对任意的 ,限 0 < ε < 0.01。当然可以!但是,作为定义不能这样叙述,否则,张三限制0 < ε < 0.01 ,李四限制 0 < ε < 0.05,不是乱了套吗?所以作为统一的定义还是“对于任意的正数 ε ”的用语为妥。不过许多高等数学教材中极限定义都对ε > 0加了定语或附注,如“无论正数ε 多么小”、“对于任意小的 ε > 0”等,道理就在于此。那么可否将ε > 0 的任意性理解成为“无穷多个ε > 0 ”?否!“无穷多个ε > 0 ”可能把 ε限制成大于某个正数,而丢掉了“无论多么小的 ε > 0”。如限制![]() ,就丢掉了
,就丢掉了![]() 中的所有 ε,所以这样理解是错误的。不过,如果限制ε > 0 为一趋于零的正数列,比如
中的所有 ε,所以这样理解是错误的。不过,如果限制ε > 0 为一趋于零的正数列,比如![]() ,存在 δ,则对任意其他的ε ,总可以找到 ,此时,同一个 δ照样实用。
,存在 δ,则对任意其他的ε ,总可以找到 ,此时,同一个 δ照样实用。
(3)定义中的 δ不是任意的。从定义中可知, δ并不唯一,比如证明极限 ![]() ,即证明对于任意的ε > 0 ,使不等式|(x2+l)-1|< ε 成立的x 的变化范围0< |x-x0|< δ 的存在,亦即证明 δ > 0 的存在。由|(x2+1)-1|<|x2| < ε,这只要
,即证明对于任意的ε > 0 ,使不等式|(x2+l)-1|< ε 成立的x 的变化范围0< |x-x0|< δ 的存在,亦即证明 δ > 0 的存在。由|(x2+1)-1|<|x2| < ε,这只要 ![]() ,故可取
,故可取![]() 。当然也可取
。当然也可取![]() ,如此看来 δ有无穷多个。
,如此看来 δ有无穷多个。
![]() ,也就是函数
,也就是函数![]() 当
当![]() 时不以a为极限。我们知道
时不以a为极限。我们知道![]() 的分析定义是:
的分析定义是:
![]() ,它的否定就是:
,它的否定就是:
![]() ,也就是说,对所有实数域里面的数a,都存在正数ε,对所有的正数的
,也就是说,对所有实数域里面的数a,都存在正数ε,对所有的正数的![]() 总存在这样的X,它满足条件
总存在这样的X,它满足条件![]() ,但是
,但是![]() 。
。
不是。按照函数的定义,对于给定的自变量要有确定的因变量与它对应才成为函数关系。在我们的定义中,给定![]() 以后,我们可以取的
以后,我们可以取的![]() 有无限多的可能,事实上只要我们找到一个
有无限多的可能,事实上只要我们找到一个![]() 满足定义要求,则所有
满足定义要求,则所有![]() 都是与
都是与![]() 对应的满足定义条件的
对应的满足定义条件的![]() ,具有不确定性,因此不能认为是函数关系。
,具有不确定性,因此不能认为是函数关系。
是判定极限的存在性,如果不能确定极限存在就容易出现下例的错误。
例:设![]() ,求
,求![]()
解:记![]() ,对等式
,对等式![]() 两边取极限,得
两边取极限,得![]() ,
,
从此得出![]() ,所以
,所以![]()
由极限的保号性,这个结论显然是错的,问题出在只有极限存在时才能记![]() ,也才能对等式
,也才能对等式![]() 两边取极限。
两边取极限。
不对。例如![]() 在区间
在区间![]() 内都是无界的,但是
内都是无界的,但是![]() 是有界的。
是有界的。
参照定义我们知道无穷小的阶总是与等价无穷小相联系的,它是一个相对的概念。特别地,如果当![]() 时
时![]() 是关于
是关于![]() 的
的![]() 阶无穷小,那末就简称
阶无穷小,那末就简称![]() 是当
是当![]() 时的
时的![]() 阶无穷小;如果当
阶无穷小;如果当![]() 时
时![]() 是关于
是关于![]() 的
的![]() 阶无穷小,那末就简称
阶无穷小,那末就简称![]() 是当
是当![]() 时的
时的![]() 阶无穷小。
阶无穷小。
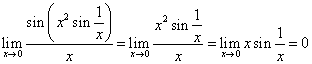 对吗?
对吗?结论正确但是过程在第一步就错了。原因是第一个等式实际上用了等价无穷小的替换的概念,而它们并不是等价无穷小的关系。正确的解法是用夹逼准则,
因为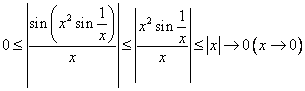 ,所以
,所以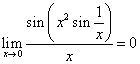
关于高阶无穷小,有如下运算规律:当![]() 时,
时,
= 1 \* GB2⑴![]() ;
;
= 2 \* GB2⑵当![]() 时,
时,![]()
= 3 \* GB2⑶![]()
= 4 \* GB2⑷设![]() 有界,则
有界,则![]()
这里要注意的是两类容易出的错误:= 1 \* GB3①认为![]() 是错的;= 2 \* GB3②认为
是错的;= 2 \* GB3②认为![]() 也是错的,请看例子:
也是错的,请看例子:![]() ,
,![]() ,但
,但![]() 根本就不是
根本就不是![]() 的无穷小量,而是
的无穷小量,而是![]() 的无穷
的无穷